Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 8.Questões e Problemas - Ex. 19b
A água pode ser determinada em amostras sólidas por espectroscopia no infravermelho. O conteúdo de água do sulfato de cálcio hidratado deve ser medido empregando-se carbonato de cálcio como padrão interno para compensar alguns erros sistemáticos do procedimento. Uma série de soluções padrão contendo sulfato de cálcio diidratado e uma quantidade constante conhecida do padrão interno é preparada. A solução com conteúdo desconhecido de água também é preparada contendo a mesma quantidade do padrão interno. A absorbância do composto diidratado é medida em um comprimento de onda () juntamente com aquela do padrão interno em outro comprimento de onda (). Os seguintes resultados foram obtidos.
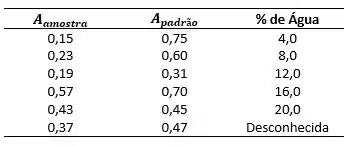
- Faça um gráfico da razão % de água e comente se o uso do padrão interno melhora a linearidade obtida na parte (a). Se há melhoria na linearidade, explique por quê.
Passo 1
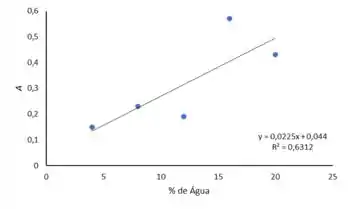
Oi galerinha. Para a gente construir o gráfico, iremos utilizar o programa Excel, mas fiquem calmos que irei te ajudar. Do item (a), obtivemos o seguinte resultado:
E para este exercício iremos considerar que:
;
.
Então primeiramente iremos calcular a relação da absorbância da amostra com o padrão:
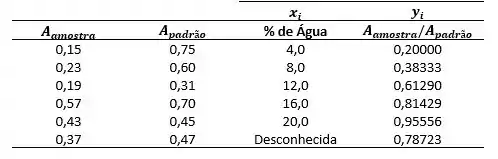
Passo 2
Agora conseguimos construir nosso gráfico. Para isso iremos selecionar os dados:
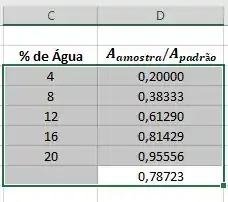
Então clicamos na aba “Inserir” e na opção “Gráficos”, escolhemos “Dispersão”:
Nosso gráfico será criado e precisamos colocar a linha de tendência linear. Iremos clicar no símbolo () à direita do gráfico, selecionar a opção “Linha de Tendência” e escolher a opção “Linear”, como está descrito abaixo:
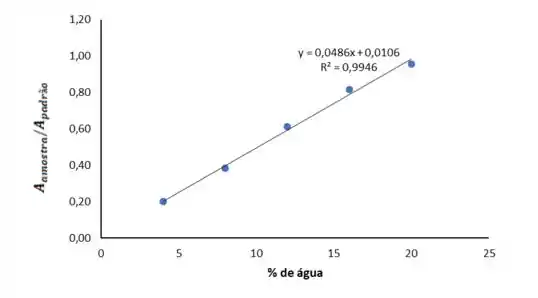
E assim iremos obter o gráfico a seguir:
Passo 3
Com isso temos o valor do coeficiente de correlação:
E nossa equação da reta:
Onde:
Inclinação da reta: ;
Intercepto: .
Pelo gráfico conseguimos perceber que o ajuste linear melhorou muito em comparação com o obtido no item (a), além de ser visual, o valor do coeficiente de correlação aumentou bastante e obtivemos um bom valor ().
Passo 4
Além do coeficiente de variação (), conseguimos determinar também o valor pela equação:
Para chegarmos neste valor, vamos fazer alguns cálculos primeiramente, como uma amostra é desconhecido, iremos considerar :
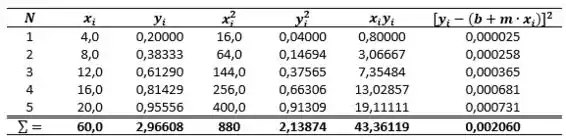
Onde, temos a soma dos quadrados:
A soma total dos quadrados tem quatro graus de liberdade associados a ela. A soma dos quadrados devido aos resíduos possui três graus de liberdade. Além disso, tem apenas um grau de liberdade.
Agora iremos calcular o valor de , porque ele nos indica a significância da regressão:
Como nosso valor é grande, indica que nossa hipótese nula deve ser rejeitada e que a regressão é significativa. Ou seja, só confirmamos o que foi já tínhamos percebido, que o ajuste linear melhorou.
Pelo gráfico conseguimos perceber que o ajuste linear melhorou muito em comparação com o obtido no item (a), além de ser visual, o valor do coeficiente de correlação aumentou bastante e obtivemos um bom valor ().
Prontinho pessoal, espero que tenha conseguido te ajudar, até mais.
Resposta
Faça um gráfico da razão % de água e comente se o uso do padrão interno melhora a linearidade obtida na parte (a). Se há melhoria na linearidade, explique por quê.
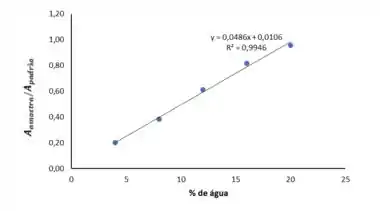
Além de percebermos, visualmente, uma melhora no ajuste linear, também é possível notar pelos valores altos do coeficiente de correlação () e do valor (). Fazendo a razão da absorbância da amostra com o padrão, nós conseguimos anular os erros sistemáticos que afetam a amostra e o padrão.