Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 3
3 – Antes de fazer o cálculo a seguir, esquematize a dependência da superposição entre um orbital 1s e um orbital 2p com a distância entre os dois orbitais. A integral de superposição entre um orbital H1s e outro H2p, em núcleos separados pela distância R e formando um orbital σ, é dada por
Faça o gráfico dessa função e ache a distância na qual a superposição é máxima.
Passo 1
O orbital s começa a se espalhar na região da amplitude negativa do orbital p. Quando seus centros coincidem, a região de superposição positiva cancela a região negativa.
Usando a expressão fornecida pelo enunciado, podemos montar a seguinte tabela de valores para a integral de superposição, S:
Passo 2
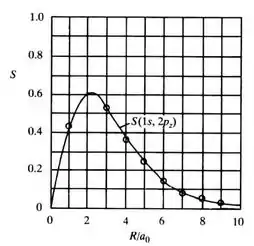
Com os dados da tabela acima, podemos plotar o seguinte gráfico da integral de superposição em relação a R/a0:
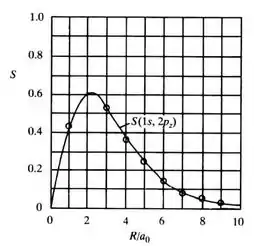
Pelo gráfico, podemos observar que o valor de R/a0 pelo qual a integral de superposição é máxima, ocorre em, aproximadamente:
Assim, o raio para o máximo valor de S é:
Resposta
Máximo S:
