Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 6.Questões e Problemas - Ex. 16
No Capítulo 24 vamos mostrar que a espectrometria de absorção molecular quantitativa
baseia-se na lei de Beer, que pode ser escrita como
em que é a transmitância de uma solução contendo o analito , é a espessura da solução absorvente, é a concentração molar de e é uma constante determinada experimentalmente. Por meio da medida de uma série de soluções padrão de , teve seu valor determinado como , no qual o número entre parênteses representa o desvio padrão absoluto.
Uma solução de de concentração desconhecida foi medida em uma célula idêntica àquela usada para determinar . As réplicas dos resultados foram . Calcule:
(a) a concentração molar do analito ;
(b) o desvio padrão absoluto para ;
(c) o coeficiente de variação para .
Passo 1
Oi galerinha, do enunciado temos os seguintes dados:
;
.
E queremos descobrir , então a equação fica:
Então iremos calcular a média e o desvio padrão da transmitância:
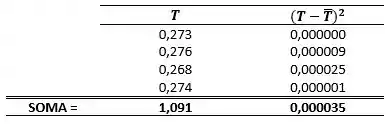
A média será:
Com isso já conseguimos calcular o item (a):
Passo 2
Para o cálculo do item (b) precisamos do desvio padrão da transmitância:
Então temos que:
;
.
E temos a equação da concentração da seguinte maneira:
Primeiramente precisamos calcular o desvio padrão para o logaritmo, onde temos as seguintes equações:
Agora temos a equação da seguinte maneira:
Porém agora precisamos estimar o desvio padrão deste resultado para o desvio padrão de um produto ou consciente:
Então:
Passo 3
E por fim, no item (c) queremos o coeficiente de variação:
Até mais pessoal.
Resposta
- .
- .