Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 11.Problemas Numéricos - Ex. 9
9 – Os dados do Problema 11.8 servem para calcular a curva da energia potencial da molécula no orbital antiligante, cuja expressão é dada por
Faça o gráfico da curva.
Passo 1
Como foi pedido para usarmos os dados do problema 11.8 para plotarmos o gráfico da curva da energia potencial, precisaremos colocar a expressão da energia potencial, E, em termos das variáveis que possuem valores conforme os dados do problema 11.8.
Os dados do problema 11.8 são:
Assim, vamos colocar a expressão de E em termos das variáveis da imagem acima.
Passo 2
Sendo a expressão:
Fazendo
Dividindo a eq. acima por Eh:
Rearranjando,
Passo 3
Pegando o termo
Por manipulação algébrica:
Por definição temos que, pela Eq. 10.13 do Atkins:
Assim,
Também por definição, pela Eq. 10.15:
Assim,
Fazendo
Como
Assim,
Passo 4
Com a relação mostrada anteriormente, podemos escrever a Eq2 da seguinte forma:
Agora temos uma expressão que fica em função apenas dos dados do problema 11.8, que podemos fazer um gráfico de
Passo 5
Plotando a curva de E com os seguintes dados:
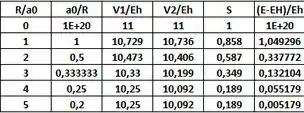
Obteve-se o seguinte gráfico:
Resposta
