Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 13.1 - Ex. 41

Determine o potencial das seguintes células

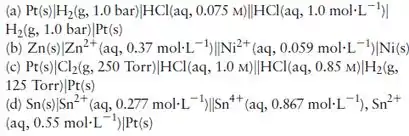
Passo 1

Bora começar mais umaa!

Queremos o potencial, e como podemos calcular?

Fácil!

E_c é l u l a = E^0_c é l u l a - (R T)/(n F) . ln Q

O termo (R T)/(n F) é constante, não é? E já vou colocar o valor aqui pra vocês :

E_c é l u l a = E^0_c é l u l a - (0,025693 V)/(n) . ln Q

E este Q aí? Calma que eu também mostro:

Q = ([E s p é c i e]_P r o d u t o s)/([E s p é c i e]_R e a g e n t e)

Como nós temos o o HCl concentrado originando o diluído:

Q = ([H C l]_d i l u i d o)/([H C l]_C o n c e n t r a d o) = (0,075)/(1,0) = 0,075

Agora só falta calcular o potencial padrão e o número n de elétrons.

Como nossas espécies envolvidas trocam somente um elétron, n = 1 .

Se nós temos dois eletrodos iguais o potencial padrão será: E^0_c é l u l a = 0 .

Substituindo:

E_c é l u l a = 0 - (0,025693 V)/(1) . ln 0,075

E_c é l u l a = + 0,067 V

E pronto ! Achamos o potencial ! Agora faremos o mesmo procedimento nas demais letras, ok?

Passo 2

Para a letra b a equação geral será:

N i^(2 +) + Z n -> N i + Z n^(2 +)

Como N i^(2 +) se reduz a N i e Z n se oxida a Z n^(2 +) .

Colocando as meias-reações:

C a t o d o : N i^(2 +) + 2 e^- -> N i E^0 = - 0,23 V

A n o d o : Z n -> Z n^(2 +) + 2 e^- E^0 = - 0,76 V

Se o potencial padrão da célula é:

E^0_c é l u l a = E^0_C - E^0_A

Substituindo:

E^0_c é l u l a = - 0,23 - ( - 0,76 ) = 0,53 V

Para o Q nós teremos:

Q = ([Z n^(2 +)])/([N i^(2 +)]) = (0,37)/(0,059) = 6,3

E:

n = 2

Substituindo:

E_c é l u l a = 0,53 V - (0,025693 V)/(2) . ln 6,3

E_c é l u l a = + 0,51 V

Passo 3

A letra c nós temos

H^+ + C l^- + H C l -> H_2 + C l_2 + H C l

Como H^+ se reduz a H_2 e C l^- se oxida a C l_2 .

Colocando as meias-reações:

C a t o d o : 2 H^+ + 2 e^- -> H_2 E^0 = 0 V

A n o d o : 2 C l^- -> C l_2 + 2 e^- E^0 = + 1,36 V

Na equação geral:

2 H^+ + 2 C l^- -> C l_2 + H_2

Se o potencial padrão da célula é:

E^0_c é l u l a = E^0_C - E^0_A

Substituindo:

E^0_c é l u l a = 0 - 1,36 = - 1,36 V

E:

n = 2

Transformando a pressão de Torr em bar, dividindo por 760, e colocando em Q:

Q = (P_H_2 P_C l_2)/([H C l]^2_R . [H C l]^2_P) = ((125)/(760) xx (250)/(760))/(0,85^2 xx 1^2) = 0,07 5

Fizemos essa transformação para igualar as unidades na razão galera! E usamos a concentração do HCl porque foi ele que gerou os íons, certo?

Substituindo:

E_c é l u l a = - 1,36 V - (0,025693 V)/(2) . ln 0,07 5

E_c é l u l a = - 1,33 V

Passo 4

Para finalizar com chave de ouro:

S n^(4 +) ( 0,867 ) + S n -> S n^(2 +) ( 0,55 ) + S n^(2 +) ( 0,277 )

Como S n^(4 +) se reduz a S n^(2 +) e S n se oxida a S n^(2 +) .

Colocando as meias-reações:

C a t o d o : S n^(4 +) + 2 e^- -> S n^(2 +) E^0 = + 0,15 V

A n o d o : S n -> S n^(2 +) + 2 e^- E^0 = - 0,14 V

Se o potencial padrão da célula é:

E^0_c é l u l a = E^0_C - E^0_A

Substituindo:

E^0_c é l u l a = 0,15 - ( - 0,14 ) = 0,29 V

Para o Q nós teremos:

Q = ([S n^(2 +)] [S n^(2 +)])/([S n^(2 +)]) = (0,277 xx 0,55)/(0,867) = 0,178

E:

n = 2

Substituindo:

E_c é l u l a = 0,29 V - (0,025693 V)/(2) . ln 0,178

E_c é l u l a = + 0,31 V

E é isso aí !!

Resposta

  1. E_c é l u l a = + 0,067 V ;
  2. E_c é l u l a = + 0,51 V ;
  3. E_c é l u l a = - 1,33 V ;
  4. E_c é l u l a = + 0,31 V .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

111. Quando um medidor de p H foi padronizado com uma solução tamáo ácido bórico-borato com p H = 9,40 , o potencial de célula atingiu +0,060V. Quando o tampao foi substituído por uma solução de conce
110. Qual é o potencial padrão da redução de oxigênio a água em (a) uma solução ácida? (b) uma solução básica? Será que MnO4- é mais estável em uma solução aerada ( uma solução saturada com gas oxigên
109. Use dados do apêndice 2B para determinar o potencial padrão da reação redox 2 A g + a q + 2 I - a q → 2 A g s + I 2 s . Este processo é espontâneo em condições padrão? (b) Quando volumes iguais d
121. Muitas reações biológicas importantes envolvem transferência de elétrons. Como o p H dos fluidos corporais está próximo de 7, o ´´ potencial biológico padrão´´ de um eletrodo, E°, é ,medido em p
Examine novamente a questão proposta no Exercício 13.51 imaginando, porém, que um eletrodo de calomelano saturado (a solução é saturada com K C l em vez de ter C l - =1,00m o l . L - 1 ) substitui o e