Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 8.1 - Ex. 95

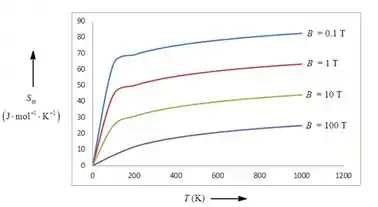
A entropia molar dos spins dos elétrons em um campo magnético B é

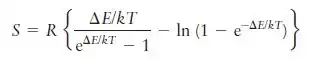
onde ∆ E = 2 μ B B é a diferença de energia entre dois estados de spin em um campo magnético, μ B é o magneton de Bohr, igual a 9,274 × 10 - 24 J . T - 1 . Faça um gráfico desta função contra a temperatura para os seguintes valores de B: 0,1   T ;   1   T ;   10   T   e   100   T . (Veja o Quadro 8.1. Observe que a unidade de indução magnética, o tesla, T, em que 1   T = 1   k g . s - 2 .   A - 1 , cancela).

Passo 1

Essa é trabalhosa galera, então vamos com calma!

Já sabemos que a entropia é calculada como:

S = R ∆ E k T e ∆ E k T - 1 - ln ⁡ ( 1 - e - ∆ E k T )

Sabemos que:

μ B = 9,274 × 10 - 24 J T e s l a

k = 1,381 × 10 - 23 J K  

R = 8,314 J m o l .   K

Então:

∆ E = 2 9,274 × 10 - 24 J T e s l a B = 1,855 × 10 - 23 J T e s l a B

∆ E k T = 1,855 × 10 - 23 J T e s l a B 1,381 × 10 - 23 J K T = 1,343 K T e s l a   B T

Para B = 0,1   T e s l a :

∆ E k T = 1,343 K T e s l a   0,1   T e s l a T = 0,1343   K T

S = 8,314 J m o l .   K 0,1343   K T e 0,1343   K T - 1 - ln ⁡ ( 1 - e - 0,1343   K T )

Olhando os valores de entropia com a temperatura de 100 – 1000 K:

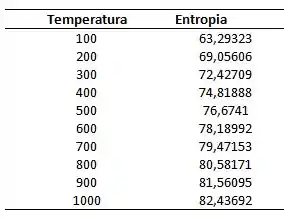
Passo 2

Para B = 1   T e s l a :

∆ E k T = 1,343 K T e s l a   1   T e s l a T = 1,343   K T

S = 8,314 J m o l .   K 1,343   K T e 1,343   K T - 1 - ln ⁡ ( 1 - e - 1,343   K T )

Olhando os valores de entropia com a temperatura de 100 – 1000 K:

Passo 3

Para B = 1 0   T e s l a :

∆ E k T = 1,343 K T e s l a   1 0   T e s l a T = 1 3 , 43   K T

S = 8,314 J m o l .   K 1 3 , 43   K T e 1 3 , 43   K T - 1 - ln ⁡ ( 1 - e - 1 3 , 43   K T )

Olhando os valores de entropia com a temperatura de 100 – 1000 K:

Passo 4

Para B = 1 0 0   T e s l a :

∆ E k T = 1,343 K T e s l a   10 0   T e s l a T = 134 , 3   K T

S = 8,314 J m o l .   K 134 , 3   K T e 134 , 3   K T - 1 - ln ⁡ ( 1 - e - 134 , 3   K T )

Olhando os valores de entropia com a temperatura de 100 – 1000 K:

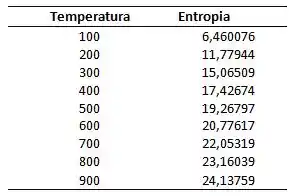
Passo 5

Agora vamos lançar tudo isso no gráfico:

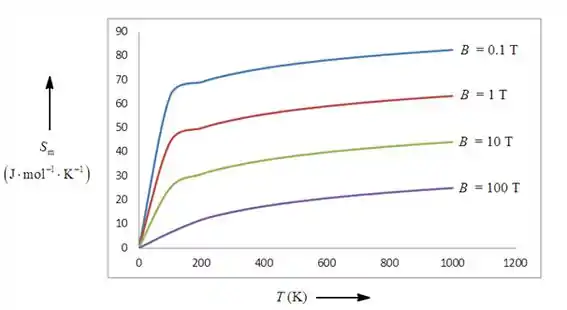
O que acharam desta?

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8.22 (a) Use a regra de Trouton para estimar o ponto de ebulição do metilamina, C H 3 N H 2 , sabendo que ∆ H v a p o = 35,60k J / m o l . (b) Use as fontes de referência disponíveis em sua biblioteca
As populações p dos estados de spin para cima e para baixo em um campo magnético B são dadas:Em que ∆ E = 2 μ B B é a diferença de energia entre os dois estados de spin (consulte o Exercício 8.95). La
Suponha que fosse possível conseguir que houvesse duas vezes mais elétrons com spins para cima do que para baixo em um campo magnético. Sem fazer nenhum cálculo, prediga o sinal da temperatura na amos
Sem fazer nenhum cálculo, prediga que temperatura corresponde a populações iguais de estados de spin para cima e para baixo. (Ver Exercício 8.96).