Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 1.1 - Ex. 59

Escreva a notação da subcamada (3d, por exemplo) e o número de orbitais que têm os seguintes números quânticos: (a) n = 5, l = 2; (b) n = 1, l = 0; (c) n = 6, l = 3; (d) n = 2, l = 1.

Passo 1

Em primeiro lugar, vamos determinar a subcamada (3d, 4s, 7p, etc, por exemplo). Pra isso, vamos identificá-la justamente a partir do , número quântico principal, e também de , número quântico secundário, ou azimutal, ou de momento angular.

Esses números já estão dados em cada item, então fácil determinar a subcamada: o primeiro número é exatamente o dado, já o tipo de orbital da subcamada vai ser indicado por , sendo identificado por seu número. Mas, claro, se você não lembra, as tabelas abaixo correlacionam o número quântico secundário, e seus números correspondentes:

Tendo essas informações à disposição, teremos:

(a) 5d

(b) 1s

(d) 2p

Passo 2

Agora, pra sabermos quantos orbitais temos em cada subcamada dessas, também é muito simples: vemos pela tabela abaixo a quantidade de “casinhas” que cada tipo de orbital tem:

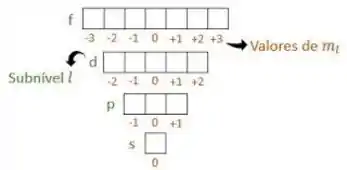
(a) Se a subcamada é nd, temos 5 orbitais d.

(b) Se a subcamada é ns, temos 1 orbital s.

(d) Se a subcamada é np, temos 3 orbitais p.

Resposta

(a)5d; 5 orbitais.

(b)1s; 1 orbital.

(d)2p; 3 orbitais.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

119. A intensidade de uma transição entre os estados nen ´ de uma partícula em uma caixa é proporcional ao quadrado da integral I , em que I n n ´ = ∫ 0 L Ψ n Ψ n ´ d x Será que pode ocorrer uma trans

117. As funções de onda que correspondem a estados de energia diferente da partícula em uma caixa são mutuamente ´´ ortogonais´´, no sentido que, se as duas funções de onda são multiplicadas, uma pela

118. As funções de onda são ´´ normalizadas´´ a 1. Isso significa que a probabilidade de encontrar um elétron no sistema é 1. Verifique essa afirmação para uma função de onda da partícula em uma caixa

130. Este gráfico mostra a função de distribuição radial dos orbitais 3s e 3p do átomo de hidrogênio. Identifique as curvas e explique como tomou a decisão.

Quais são os números quânticos principal e de momento angular do orbital para cada um dos seguintes orbitais: (a) 6p; (b) 3d; (c) 2p; (d) 5f?