Exercício Desafiador. De acordo com Kenny et al.,3 o número de Avogadro NA pode ser calculado com base na seguinte equação, usando medidas realizadas em uma esfera fabricada a partir de um monocristal ultrapuro de silício.
Passo 1
Beleza Pessoal?! Espero que sim, me chamo Yuri e hoje iremos dar início a mais uma resolução com o padrão de qualidade do responde aí, vem comigo!!!
Neste exercício, devemos considerar o método, que inclui a fabricação de um cristal único ultrauso de silício, levando à determinação precisa do número de Avogadro. Após a implementação do método, a seguinte fórmula foi deduzida
![]()
O parâmetro de rede de cristal elevado à potência de 3 é igual ao volume de uma célula de unidade
- Nesta parte, devemos derivar a fórmula acima mencionada para o número de Avogadro. Em primeiro lugar, a partir da dimensão do número de Avogadro, sabemos, que é inversamente proporcional ao número de mols de uma matéria, que é o silício no nosso caso:
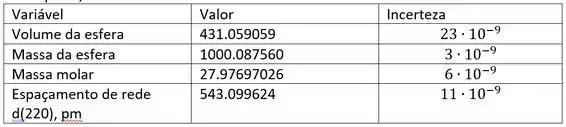
- Nesta parte, devemos calcular a densidade do silício e a incerteza da tabela abaixo:
- Nesta parte, devemos determinar o número de Avogadro pela equação dada, e a incerteza do valor. Em primeiro lugar, no entanto, devemos converter os valores relacionados ao volume em uma unidade. Como o volume de silício é dado em cm^33, vamos converter o espaçamento da rede (aa) para cm também. Os valores obtidos derivam da tabela esboçada no Passo 6.
- Nesta parte, devemos determinar o número de Avogadro novamente, usando outro cristal. Os dados do cristal estão listados abaixo:
- Nesta parte, nomeie as variáveis que têm a influência mais significativa no cálculo do número de Avogadro e nomeie o motivo para isso. Em primeiro lugar, vamos dar outra olhada na fórmula com o volume expresso com o raio:
![]()
Como observar a estrutura cristalina o número de átomos em uma célula unitária e o volume de uma unidade no cristal é dado, vamos derivar um valor relacionado ao volume, como um próximo passo.
![]()
Isso, na verdade, é igual ao volume molar de silício.
Sabendo o volume de uma unidade de cristal, e o número de átomos que um cristal contém, podemos completar nossa expressão. O volume molar (V_{\text{mol}}Vmol) dividido pelo volume de uma unidade (a^3a3) rende o número de unidades em uma toupeira de cristal. Multiplicar essa expressão pelo número de átomos (n) em uma unidade produz o número de Avogadro.
![]()
O volume de uma substância também pode ser expresso como a fração de sua massa e densidade.
![]()
Em termos de valores molares, o volume muda para volume molar, e a massa muda para massa molar:
![]()
Substituamos esta expressão à fórmula na :
![]()
Como ρ também pode ser expressado por massa e volume (ρ=m/V), vamos substituir essas variáveis na expressão do número de Avogadro:
![]()
Esta expressão é a mesma especificada na descrição da tarefa
Passo 2
A densidade pode ser calculada de acordo com a seguinte fórmula:

A incerteza do valor pode ser dada pela fórmula utilizada para calcular o desvio padrão para produtos/quocientes (como y=ab/c).
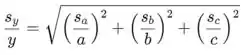
onde os valores s referem-se às incertezas correspondentes (desvio padrão) e as letras representam os valores.
De acordo com isso, no nosso caso, a incerteza da densidade do silício é dada da seguinte forma:
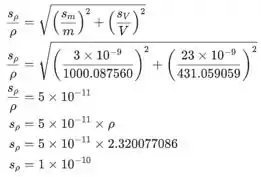
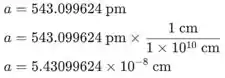
À medida que convertemos o valor em si, o valor de incerteza também deve ser convertido para os cálculos adicionais:
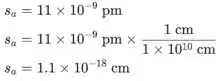
Usemos a fórmula dada para a determinação do número de Avogadro:

A incerteza do valor pode ser dada pela fórmula utilizada para calcular o desvio padrão para produtos/quocientes (como y=ab/c).
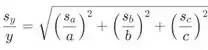
onde o valors refere-se às incertezas correspondentes (desvio padrão) e as letras representam os valores.
De acordo com isso, no nosso caso, a incerteza do número de Avogadro é dada da seguinte forma:

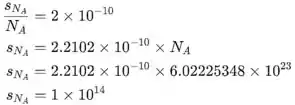

Vamos usar a fórmula dada para a determinação do número de Avogadro. Como neste caso, não o volume, mas o raio da esfera é dado, vamos incluir a expressão usada para calcular o volume de uma esfera. Além disso, devemos ter em mente que o espaçamento de rede dado o gás não é considerado a correção da geometria cristalina, por isso, para obter o valor de a, devemos usar o coeficiente correspondente

A incerteza do valor pode ser dada pela fórmula utilizada para calcular o desvio padrão para produtos/quocientes (como y=ab/c).
![]()
onde o valors refere-se às incertezas correspondentes (desvio padrão) e as letras representam os valores.
De acordo com isso, no nosso caso, a incerteza do número de Avogadro é dada da seguinte forma:
![]()
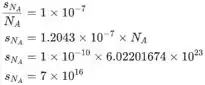
Como próximo passo, vamos determinar o valor médio dado pelas duas variáveis, pois será necessário determinar se a diferença entre elas é estatisticamente significante.

Para determinar se dois valores são estatisticamente significativos, a melhor opção é realizar um teste t. Apesar de não termos nenhuma hipótese nula, vamos realizar o teste e estimar o intervalo de confiança. O intervalo de confiança correspondente mostra o quão próximos os valores numé somais do Avogadro estão um para o outro. Quanto menor o valor do intervalo de confiança, menor a diferença entre os dois valores.
Como o sistema de interesse é um sistema de duas amostras, o desvio padrão das duas amostras será igual um ao outro. Em primeiro lugar, vamos calcular esse valor.
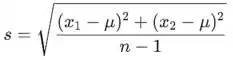
![]()
Passo 3
Conhecendo o desvio padrão, vamos realizar o teste t.

Isso significa que a curva gaussiana relacionada mostraria que o nível de confiança correspondente seria inferior a 50%. Portanto, os dois valores são de fato muito próximos um do outro, e podemos afirmar que a diferença entre eles não é estatisticamente significante. Assim, o valor médio previamente calculado ( 1/mol) pode ser aceito.
A incerteza de uma média é dada pelas incertezas correspondentes dos respectivos valores de acordo com a seguinte fórmula, que é usada para determinar a incerteza das somas:
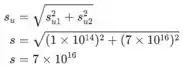
Isso significa que a incerteza do valorde é de .
![]()
Como podemos ver, há duas variáveis que são em cubos, uma delas é o valor do espaçamento da treliça, e a do raio do cristal. Isso significa que a expressão para o número de Avogadro é muito sensível à mudança desses parâmetros, ou seja, eles têm a maior influência sobre o resultado.
f) Neste exercício, devemos nomear os métodos experimentais utilizados para fazer as medições mostradas na tabela.
A formação e o crescimento de cristais de silício podem ser realizados pelas chamadas técnicas de deposição de vapor químico (CVP) e zona flutuante, onde o silício é depositado na superfície do produto. A pureza do silício deve ser fornecida por várias técnicas de polimento para remover as camadas de óxido formadas do cristal. O diâmetro do silício formado foi medido por interferometria óptica, que é um bom meio de determinação da topografia superficial.
A medição precisa e precisa da massa também é de vital importância, que foi realizada pelo equilíbrio padrão de 2 kg de Sartorius no ar. A massa molar do silício foi determinada pela espectrometria de massa, que usa o método de separação de diferentes velocidades de migração das espécies ionizadas quando elas têm diferentes relações carga-massa (na verdade, massa diferente). A medição do parâmetro de rede foi realizada pela cristalografia de raios-X, que fornece um excelente método para determinar, e criar as estruturas de moléculas versáteis.
Passo 2
g) Nesta parte, devemos comentar variáveis experimentais que podem contribuir para a incerteza da medida. Como em parte e), em primeiro lugar, vamos dar outra olhada na fórmula
![]()
Como podemos ver, a densidade em si pode ter uma grande influência na precisão da medida, pois é afetada tanto pela incerteza da massa, quanto pela do volume (e, portanto, no raio).
Além das duas variáveis mencionadas, há também outros fatores que podem contribuir para a incerteza da determinação da densidade. Por exemplo, durante a formação de silício, também uma camada de óxido protetor pode ser formada na superfície do produto. Isso, embora o polimento seja aplicado, pode levar à presença de alguns traços indesejados de óxido de silício, cuja espessura e densidade podem levar a algumas fontes de incerteza.
Por outro lado, durante as medidas de interferometria óptica utilizadas para a caracterização das impurezas, alguns hidrocarbonetos também são introduzidos pelo sistema de bombeamento de vácuo operacional. Isso também pode ser uma fonte de incerteza.
Durante a formação dos cristais quase perfeitos, algumas impurezas e erros de rede também podem afetar a precisão da medição em termos do parâmetro de rede e espaçamento.
Além disso, embora o método de espectrometria de massa seja uma tecnologia muito precisa, também pode ter alguns erros intrínsecos, e isso também é um fator na incerteza geral.
h) Neste exercício, devemos sugerir formas de melhorar a determinação do número de Avogadro.
Embora existam algumas incertezas que não podem ser evitadas (como a precisão da espectrometria de massa), alguns efeitos causadores de erros podem ser evitados. Por exemplo, o silício formado poderia ser mantido em uma atmosfera inerte e sem oxigênio, a fim de minimizar a formação de uma camada de óxido. No entanto, o experimento realizou um grande nível de precisão em termos da pureza do silício e da formação da esfera quase perfeita. Isso significa que, com medidas simples, não há muito espaço para melhorias.
Por outro lado, uma boa maneira de melhorar os resultados é um grande número de repetições do experimento, onde um grande número de esferas é formada e o número final do Avogadro é dado como a média do número de experimentos separados de Avogadro.
i) Nesta parte, devemos considerar o valor aprovado da constante da Avogadro e compará-lo com nossos valores computados. O valor pode ser encontrado no site da NIST, entre os valores "Constantes Físicas Fundamentais". O número atualmente aceito do Avogadro (determinado em 2018) é o seguinte:
Quanto à incerteza, o valor é escrito como exato (sem incerteza). O número de Avogadro dado pela média de nossas medições é o seguinte:
A diferença entre os dois valores é de . Isso significa que nosso valor é de alta precisão. Essa discrepância pode ser atribuída às incertezas das variáveis necessárias para o cálculo, causadas por fatores, como camadas de óxido dificilmente caracterizadas. A melhor maneira de evitar o efeito deles é realizar um número maior de medições.
j) Nesta parte, devemos mencionar os desenvolvimentos tecnológicos nas últimas décadas que levaram à fácil disponibilidade do silício ultrapure, e minimizar os erros associados às impurezas no silício, a fim de formar formas esferas quase perfeitas.
O desenvolvimento mais importante da tecnologia em termos de caracterização dos cristais foi o aparecimento da cristalografia de raios-X, que foi de importância decisiva na determinação precisa de estruturas cristalinas e parâmetros de treliça. Quanto à fabricação de cristais da forma desejada, os novos métodos de crescimento da zona flutuante dos cristais dentro da técnica de deposição de vapor químico e o desenvolvimento de técnicas de polimento foram a chave. Esta técnica permite que os cientistas formem cristais quase perfeitamente em forma de esfera.
Resposta
Ver o desenvolvimento