Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 4.1 - Ex. 95

Faça um gráfico da pressão contra o volume para 1   m o l (a) de um gás ideal, (b) de gás amônia e (c) de gás oxigênio na faixa V = 0,05   L a 1,0   L em 298   K . Use a equação de van der Waals para determinar as pressões dos gases reais. Compare os gráficos e explique a origem de quaisquer diferenças encontradas.

Passo 1

a) Usaremos a seguinte equação de gás ideal para calcular a pressão em função do volume:

P V = n R T

Reorganizando a equação acima da seguinte maneira a ficar explicitado a pressão:

P = n R T V

P  é pressão (a ser calculada)

V  é o volume ( 0,05 L - 1,00 L )

R  é constante do gás ideal ( 0,08206   L . a t m . K - 1 . m o l - 1   )

T  é a temperatura ( 298   K )

n  é o número de mols do gás ( 1   m o l )

A tabela a seguir mostra os valores de V para os quais P foi calculado usando a equação acima:

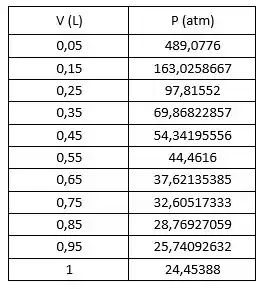
O gráfico a seguir apresenta os valores da tabela acima:

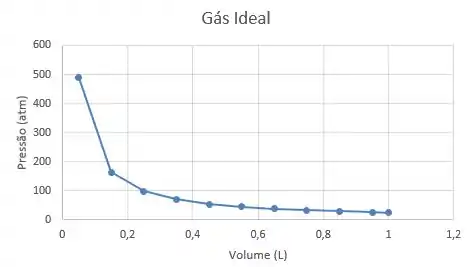
Passo 2

b) Para o cálculo da pressão do gás de amônia, a equação usada é a equação de Van der Waals,

que é:

P + a n 2 V 2 V - n b = n R T

Reorganizando a equação acima da seguinte maneira a ficar explicitado a pressão:

P = n R T V - n b - a n 2 V 2

P  é pressão (a ser calculada)

V  é o volume ( 0,05 L - 1,00 L )

R  é constante do gás ideal ( 0,08206   L . a t m . K - 1 . m o l - 1   )

T  é a temperatura ( 298   K )

n  é o número de mols do gás 1   m o l

a e b são constantes de van der Waals, para amônia, temos que:

a é 4,169   L 2 . a t m . m o l - 2  

b é 0,0371   L . m o l - 1

A tabela a seguir mostra os valores de V para os quais P foi calculado usando a equação acima:

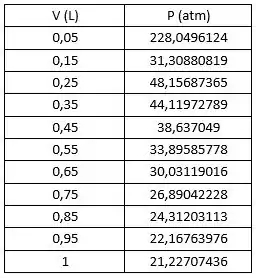
O gráfico a seguir apresenta os valores da tabela acima:

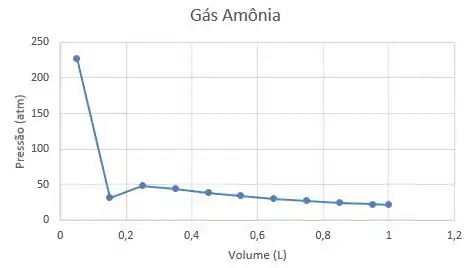
Passo 3

c) Para o cálculo da pressão do gás oxigênio, a equação usada é a equação de Van der Waals, que é:

P + a n 2 V 2 V - n b = n R T

Reorganizando a equação acima da seguinte maneira a ficar explicitado a pressão:

P = n R T V - n b - a n 2 V 2

P  é pressão (a ser calculada)

V  é o volume ( 0,05 L - 1,00 L )

R  é constante do gás ideal ( 0,08206   L . a t m . K - 1 . m o l - 1   )

T  é a temperatura ( 298   K )

n  é o número de mols do gás 1   m o l

a e b são constantes de van der Waals, para amônia, temos que:

a é 1,364   L 2 . a t m . m o l - 2  

b é 0,0319   L . m o l - 1

A tabela a seguir mostra os valores de V para os quais P foi calculado usando a equação acima:

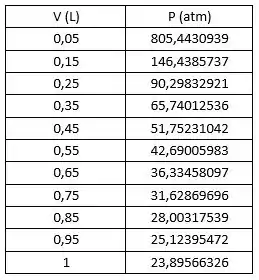
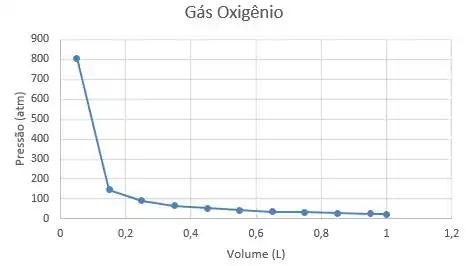
O gráfico a seguir apresenta os valores da tabela acima:

Passo 4

Combinando todos os três gráficos, o seguinte gráfico é obtido:

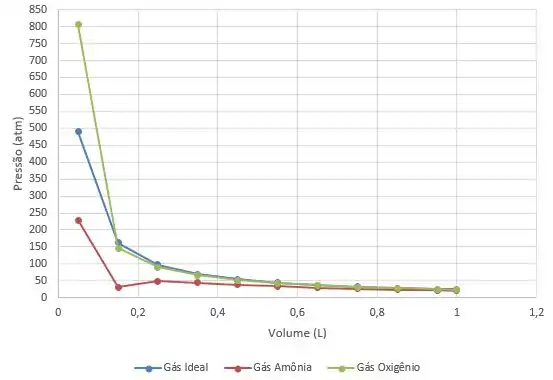
Observa-se claramente que tanto a amônia quanto o oxigênio apresentam desvios do comportamento ideal. Como a constante de Van der Waals para amônia é maior que o oxigênio, a amônia mostra um desvio maior do comportamento ideal. Isso pode ocorrer porque a amônia é polar e, portanto, possui interações intermoleculares mais fortes.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A energia de Gibbs molar de um certo gás é dada por G m = R T ln ⁡ p + A + B p + 1 2 C p 2 + 1 3 D p 3 . Em que A, B, C e D são constantes. Obtenha a equação de estado do gás.
Determine ( d S / d V ) T para (a) um gás de van der Waals; (b) um gás de Dieterci (Tabela 1.7). Para uma expansão isotérmica, para qual tipo de gás (perfeito ou real) ∆ S será maior? Explique sua con
Mostre que se B(T) for o segundo coeficiente do virial de um gás e ∆ B = B ( T )-B(T'),∆T=T - T ' , E SE T for a temperatura média entre T” e T’, então π T = R T 2 ∆ B / V m 2 ∆ T . Estime π T , a 275
Estime π T para um gás de Dieterici (Tabela 1.7). Justifique fisicamente a forma da expressão obtida.
Ache uma expressão do coeficiente de fugacidade de um gás cuja equação de estado é p V m = R T ( 1 + B V m + C / V m 2 ) . Com a expressão obtida, calcule a fugacidade do argônio a 1,00 atm e 100 K, s