Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 4.1 - Ex. 15

(a) Prepare e registre um gráfico de pressão contra temperatura para 1,00   m o l de gás, mostrando as curvas em volumes entre 0,01   L a 0,05   L em incrementos de 0,01   L para T = 0 em 400   K . (b) Qual é a expressão da inclinação de cada uma dessas linhas? (c) O que é cada intercepto? Dê suas respostas com duas casas decimais.

Passo 1

  1. Oi, galerinha! Tudo bom? Para fazer o que enunciado pede, vamos usar a equação do gás ideal:

P V = n R T

Aqui, P é a pressão, V é o volume, T é a temperatura, n é o número de mol e R é a constante dos gases ideais. Rescrevendo a equação explicitando P temos :

P = n R T V

Para cada gráfico teremos um volume constante, assim como o número de mols, a constante dos gases ideais, e vamos variar a temperatura e pressão. Ou seja, vamos construir 5 gráficos, usando volumes diferentes.

Usando a equação acima podemos obter um gráfico de pressão conta temperatura. Pra isso faremos uma planilha no Excel.

Passo 2

Para V = 0,01   L , n = 1,00   m o l , R = 0,08206   L . a t m . m o l - 1 . K - 1 e T variando 0   K a 400   K , temos a tabela para a pressão P em a t m :

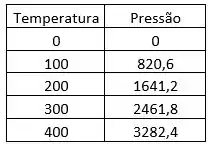
Passo 3

Para V = 0,02   L , n = 1,00   m o l , R = 0,08206   L . a t m . m o l - 1 . K - 1 e T variando 0   K a 400   K , temos a tabela para a pressão P em a t m :

Passo 4

Para V = 0,03   L , n = 1,00   m o l , R = 0,08206   L . a t m . m o l - 1 . K - 1 e T variando 0   K a 400   K , temos a tabela para a pressão P em a t m :

Passo 5

Para V = 0,04   L , n = 1,00   m o l , R = 0,08206   L . a t m . m o l - 1 . K - 1 e T variando 0   K a 400   K , temos a tabela para a pressão P em a t m :

Passo 6

Para V = 0,05   L , n = 1,00   m o l , R = 0,08206   L . a t m . m o l - 1 . K - 1 e T variando 0   K a 400   K , temos a tabela para a pressão P em a t m :

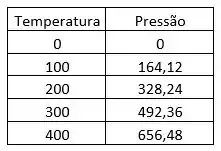
Passo 7

Acurva obtida pela plotagem de pressão conta temperatura é a seguinte:

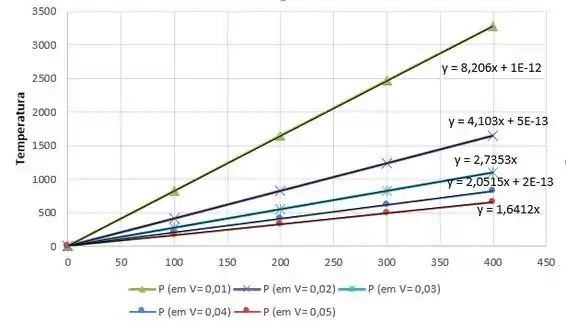
Passo 8

b) A equação do gases ideais explicitada para P , é parecida com a equação de uma reta. Em que a equação da reta é a seguinte:

y = a x + b

Comparando com a equação dos gases ideias explicitada para P :

P = n R V T

Assim podemos dizer que a inclinação para cada curva é dada pela seguinte expressão n R V . Os coeficientes angulares de cada reta, estão presente no gráfico.

Passo 9

c) Podemos perceber que os interceptos (coeficiente linear) é aproximadamente zero para todas as retas. Logo, se a temperatura tende a zero, a pressão também tenderá a zero.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

39. Ao nível do mar, onde a pressão é 104k P a e a temperatura 21,1° C , uma certa massa de ar ocupa 2,0m 3 . Até que volume ela se expandirá quando subir a uma altitude na qual a pressão e a temperat
42. Ordene os seguintes gases pela densidade crescente: N 2 , N H 3 , N O 2 . A temperatura e a pressão são as mesmas nas três amostras.
51. A densidade de um gás é 0,943g ⋅ L - 1 em 298K e 53,1k P a . Qual é a massa molar do composto?
54. A nitroglicerina é um líquido sensível ao choque, que é detonada pela reação: 4 C 3 H 5 N O 3 3 l → 6 N 2g + 10H 2 O g + 12 C O 2 g + O 2 g Calcule o volume total de gases produzido, em 215K P a e
48. A densidade do gás de um composto de fósforo é 0,943g ⋅ L - 1 , em 420K , quando sua pressão é 727T o r r .(a) Qual é a massa molar do composto?(b) Supondo que o composto permanece gasoso, qual se