Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 13.Problemas Numéricos - Ex. 11

Numa investigação do espectro de rotação do radical linear FeCO, K. Tanaka, M. Shirasaka e T. Tanaka (J. Chem. Phys. 106, 6820 (1997)) obtiveram os seguintes dados para as transições ) J + 1 ← J :

Estime a constante de rotação da molécula. Estime também o valor de para o nível de energia de rotação com maior população a 298 K e a 100 K.

Passo 1

Falaaaaaaaaaaaaaaaa Tribuxo?

Bora resolver mais uma questão!?

Vamos começar entendendo o que o exercício quer, ele quer saber a constante de rotação, para isso podemos usar:

v = 2 c B J + 1

Maaaaaaaaaaaasssssssssssssssssss, saca só o que o exercício deu de dados, UMA TABELA, e a inclinação da reta y = a + b x , é:

b = 2 c B

E para achar o nível de energia de rotação, usamos:

J m á x = k T 2 h c B 1 2 - 1 2

Bora para parte prática????

Passo 2

Vamos começar traçando um gráfico de v × J :

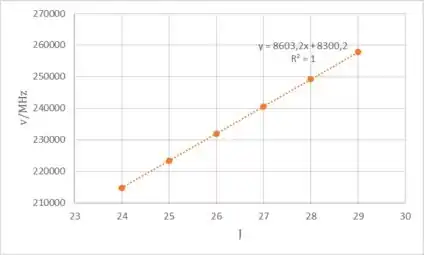
Agora vamos achar o constante de rotação, lembrando que ela é a inclinação da reta:

b = 2 c B

8603,2 = 2 c B

B = 8603,2 × 10 6 2   .   3 × 10 8

B = 14,337   m - 1

Passo 3

Agora para encontrar o J m á x :

J m á x = k T 2 h c B 1 2 - 1 2

Temos que:

b = 2 c B

Então:

J m á x = k T h b 1 2 - 1 2

Para T = 298   K :

J m á x 298   K = 1,381 × 10 - 23   .   298 6,626 × 10 - 34   .   8603,2 1 2 - 1 2

J m á x 298   K = 26,369 ≈ 26

Para T = 100   K :

J m á x 100   K = 1,381 × 10 - 23   .   100 6,626 × 10 - 34   .   8603,2 1 2 - 1 2

J m á x 100   K = 15,065 ≈ 15

Bora matar mais uma!

Resposta

B = 14,337   m - 1

J m á x 298   K = 26

J m á x 100   K = 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19a – Um radical, com dois prótons não equivalentes, com as constantes hiperfina de 2,0 mT e 2,6 mT, exibe um espectro centrado em 332,5 mT. Em que campos ocorrem as linhas do desdobramento hiperfino
1a – Qual a frequência de ressonância de um próton num campo magnético de 14,1 T?
2a – O spin nuclear do ³³S é 3/2 e o seu fator g nuclear é de 0,4289. Calcule as energias dos estados do spin nuclear num campo magnético de 7,500 T.
18a – Um radical com dois prótons equivalentes exibe um espectro de três linhas com as intensidades na razão 1:2:1. As linhas estão a 330,2 mT, 332,5 mT e 334,8 mT. Qual a constante de acoplamento hip
10a – Esboce o espectro de RMN-¹H do acetaldeído (etanal) usando J = 2,90 Hz e os dados mencionados no Exercício 15.9a, num espectrômetro que opera (a) a 250 MHz ou (b) a 500 MHz.