Enunciado
Química - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 12.Problemas Numéricos - Ex. 4
Considere a molécula H2O, que pertence ao grupo C2v. Tome como base os dois orbitais H1s e os quatros orbitais de valência do átomo de O e construa as matrizes 6 x 6 que representam o grupo nesta base. Verifique, pela multiplicação explícita das matrizes, as seguintes multiplicações no grupo: (a) e (b) . Confirme, pelo cálculo dos traços das matrizes: (a) que os elementos de simetria numa mesma classe têm os mesmos caracteres; (b) que a representação é redutível; e (c) que a base cobre 3A1+B1+2B2.
Passo 1
Opaaaaa, gente!!! Vamos usar como referência a figura 12.3 do livro. Coloque os orbitais h1 e h2 nos átomos de H e s, px, py e pz no átomo de O. O eixo x é um C2, x é perpendicular a , y está perpendicular ao plano , portanto, podemos desenhar a seguinte tabelinha abaixo ó:
Expresse as colunas encabeçadas por cada operação R na forma: (novo) = D(R)(original)
Onde D(R) seria a representação da operação R 6 X 6. Vamos usar as regras de multiplicidade de matriz!
Passo 2
Vamos lá!
(i) é reproduzido por uma matriz unitária 6 X 6
(ii) é representada pela seguinte matriz:
(iii) pela matriz:
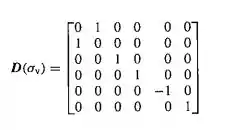
E por fim, temos que o plano é reproduzido pela seguinte matriz:
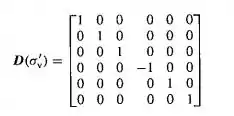
Passo 3
(a) Para confirmar a representação correta de , nós devemos escrever que:
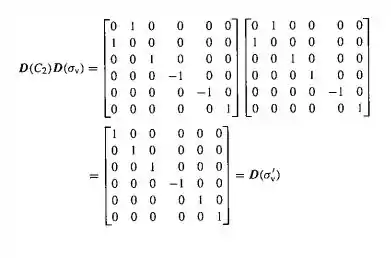
Passo 4
(b) Similarmente, para confirmar a representação correta de , escrevemos que:
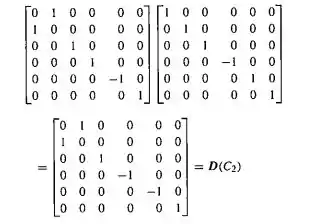
Passo 5
(a) Os caracteres de representação são os somatórios dos elementos em diagonal, certo? Portanto, temos que:
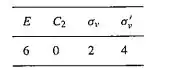
(b) Os caracteres não são aqueles de qualquer representação irredutível, logo, a representação é redutível.
(c) A soma dos caracteres de um somatório especificado é:
O qual é o mesmo como no original. Portanto, a representação é 3A1 + B1 + 2B2.
Resposta
Ei, a resposta está no passo a passo :)