Neblina poluída por fotoquímica forma-se, em parte, pela ação da luz sobre o dióxido de nitrogênio. O comprimento de onda da radiação absorvida pelo nesta reação é .
(a) Desenhe a estrutura de Lewis para e esquematize seus orbitais moleculares . (b) Após a absorção de de energia por de ar em e , todas as moléculas de desta amostra se dissociaram a partir da reação mostrada. Suponha que cada fóton absorvido leva à dissociação (em e ) de uma molécula de . Qual é a proporção, em partes por milhão, de moléculas de nesta amostra? Imagine que a amostra tem comportamento ideal.
Passo 1
a) A estrutura de Lewis é a seguinte:

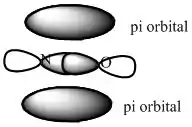
Como os orbitais pi estão presentes em e , suas sobreposições podem ser mostradas da seguinte forma:
Passo 2
b) Primeiro calculamos o número de mols de na amostra usando a equação do gás ideal:
Aqui, é a pressão, é o volume, é o número de mols de gás, é a constante dos gases ideais e é a temperatura.
Reorganizando a equação para explicitar , termos:
Onde:
é
é
é
é
Substituindo na equação acima teremos:
Portanto, o número de mols de é .
Passo 3
Uma mol de qualquer gás contém .
Calculamos então o número de moléculas de em .
Portanto, o número de moléculas de é .
Passo 4
A reação de dissociação do é a seguinte.
![]()
Podemos calcular a energia necessária para a reação acima usando a seguinte equação:
Aqui, é a energia do fóton absorvida por uma molécula de , é a constante de Planck, é a velocidade da luz e é o comprimento de onda.
Consultado o livro temos que:
é
é
é
Substituindo na equação acima:
Portanto, a energia absorvida por uma molécula de é .
Passo 5
A amostra absorveu de energia. Calculamos então o número de fótons absorvidos pela amostra.
Como o número de fótons absorvidos é igual ao número de moléculas de dissociadas, o número de moléculas de dissociadas é .
Passo 6
Calculamos agora o de dissociado, dividindo o número de moléculas dissociadas pelo total de moléculas na amostra e multiplicando por (um milhão).
Assim, a proporção de moléculas dissociadas é de .
Resposta
a)

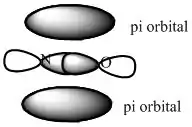
b)