Enunciado
Física - Atkins - Fisico-Quimica - Vol. 1- Ed: 8º - Capítulo 15.Problemas Numéricos - Ex. 6
6 – Pode parecer surpreendente que a equação de Karplus, deduzida para as constantes de acoplamento JHH, também se aplique ao acoplamento entre núcleos vicinais de metias como o estanho. T.N. Mitchel e B. Kowall estudaram a relação entre JHH e JSnSn em compostos do tipo Me3SnCH2RSnMe3 e descobriram que JSnSn=78,86 JHH+27,84 Hz.
A) Esse resultado justifica uma equação do tipo da de Karplus para o estanho? Explique o raciocínio.
B) Obtenha a equação de Karplus para JSnSn e faça o seu gráfico em função do ângulo de diedro.
C) Mostre qual a conformação mais favorecida.
Passo 1
Vamos rever a Eq. de Karplus, que é dada pela eq. 15.27 do Atkins:
A eq. de Karplus para JHH é:
Onde, A, B e C são constantes determinadas empiricamente cujos seus valores são:
Assim,
Então a equação acima é a equação de Karplus e para você explicar se o resultado apresentado pela equação do enunciado para JSnSn é justificável para uma equação de Karplus, o que você pode fazer é comparar o termo de JHH nas duas equações e verificar se há algum padrão de linearidade ou não linearidade com o ângulo φ.
Passo 2
A)
Na eq. de Karplus você pode perceber que JHH é linear com as funções cos(φ) e cos(2φ). Se você olhar direitinho a equação determinada experimentalmente para JSnSn você vai ver que JSnSn também é linear em relação a JHH. Dessa forma, como JSnSn é linear a JHH e JHH é linear as funções cos(φ) e cos(2φ) da eq. de Karplus, então por consequência JSnSn será linear com cos(φ) e cos(2φ). Isso então pode confirmar e justificar que a equação de Karplus pode ser aplicada para o estanho tendo a forma pela qual foi apresentada no enunciado.
Passo 3
B)
Para obtermos a equação de Karplus para o estanho, é preciso apenas substituir o parâmetro JHH pela sua relação da Eq. de Karplus.
Substituindo a eq. de Karplus para JHH na eq. determinada experimentalmente para JSnSn:
Assim,
Passo 4
Para plotarmos o gráfico vamos usar uma ferramenta gráfica, tal como o EXCEL.
Com a eq. obtida para JSnSn e atribuindo valores para o ângulo diedro de 0 a 180, obteve-se os seguintes dados para o gráfico:
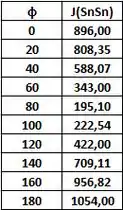
Com os dados acima, foi plotado o seguinte gráfico:
Passo 5
C)
A configuração favorecida foi a configuração representada pelos grupos trans de SnMe3 onde a repulsão é mínima.
A figura abaixo representa a configuração mais favorecida que é uma conformação trans em relação ao grupo SnMe3
Resposta
A)
Na eq. de Karplus você pode perceber que JHH é linear com as funções cos(φ) e cos(2φ). Se você olhar direitinho a equação determinada experimentalmente para JSnSn você vai ver que JSnSn também é linear em relação a JHH. Dessa forma, como JSnSn é linear a JHH e JHH é linear as funções cos(φ) e cos(2φ) da eq. de Karplus, então por consequência JSnSn será linear com cos(φ) e cos(2φ). Isso então pode confirmar e justificar que a equação de Karplus pode ser aplicada para o estanho tendo a forma pela qual foi apresentada no enunciado.
B)
C)
A configuração favorecida foi a configuração representada pelos grupos trans de SnMe3 onde a repulsão é mínima.