Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 14.1 - Ex. 103
Quais dos seguintes gráficos serão lineares?
- [A] contra o tempo em uma reação de primeira ordem em A;
- [A] contra o tempo em uma reação de ordem zero em A;
- contra o tempo em uma reação de primeira ordem em A;
- contra o tempo em uma reação de segunda ordem em A;
- k contra a temperatura;
- velocidade inicial contra [A] em uma reação de primeira ordem em A;
- meia-vida contra [A] em uma reação de ordem zero em A;
- meia-vida contra [A] para uma reação de segunda ordem em A.
Passo 1
É isso ai, galera!
Bora começar com a letra A, ok?
Para uma reação de primeira ordem, o tempo e a concentração se relacionam como:
Reorganizando:
Então o gráfico será uma exponencial. Dada como:
Ou seja, não é linear !
Passo 2
Para uma reação de ordem zero, a equação fica assim:
Bem parecido com a equação da reta, não é?
Então teremos um gráfico linear:
Passo 3
Para a letra c, a relação entre o ln da concentração e tempo nas reações de primeira ordem será dada por:
Mais uma linear:
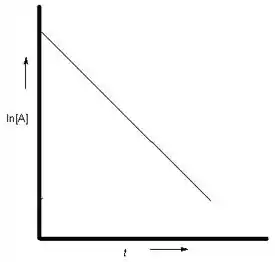
Passo 4
Em reações de segunda ordem teremos:
Também linear:
Passo 5
A constante k e a temperatura se relacionam pela Lei de Arrhenius:
Reorganizando:
Novamente, exponencial:
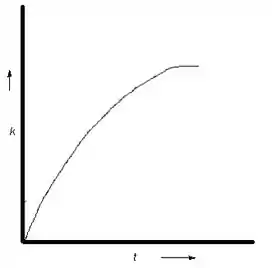
Passo 6
Qual a velocidade em uma reação de primeira ordem?
Que nos dá um gráfico linear:
Passo 7
Quase acabando galeraaa!
Vamos ver como o tempo de meia-vida se relaciona com a concentração de A em uma reação de ordem zero:
Novamente a relação é linear:
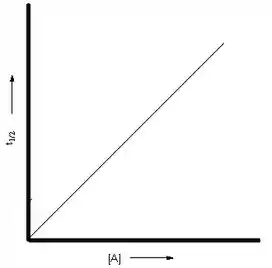
Passo 8
Vamos finalizar com a relação entre o tempo de meia vida e a concentração em reações de segunda ordem.
Neste caso a fórmula ficaria assim:
O gráfico vai ficar mais ou menos assim:
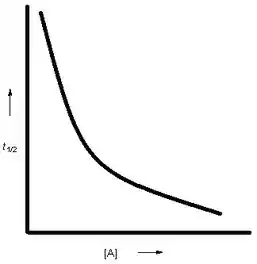
Nada de linear para essa daqui!!
Então os gráficos lineares são: b, c, d, f e g !