Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 17.1 - Ex. 13

Os seguintes nuclídeos estão fora da banda de estabilidade. Diga o tipo de decaimento preferencial de cada um deles, decaimento β - , decaimento β + ou decaimento α e identifique o núcleo-filho:

  1. cobre-68;
  2. cádmio-103;
  3. berquélio-243;
  4. dubnium-260.

Passo 1

Legal galera, vamos para mais uma!

Antes de qualquer coisa vamos precisar lembrar que:

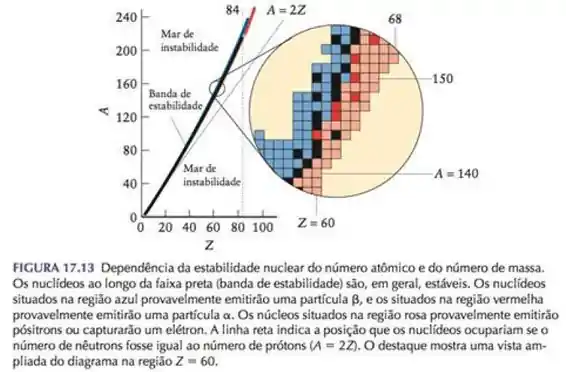
Começando pela letra a, o cobre possui:

A = 68

Z = 29

Se fizermos a razão entre ele:

A Z = 68 29 = 2,34

A = 2,34   Z

Ou seja, A > 2 Z e estamos na zona da instabilidade, acima da nossa banda de estabilidade.

Como estamos nesta região, o necleosídeo vai emitir uma partícula β .

Como vai ficar então a reação?

68 29 C u →   A Z X + 0 - 1 e

Agora vamos olhar o valor de cada uma:

68 = A + 0 → A = 68

29 = Z - 1 → Z = 30

Qual elemento tem número atômico igual a 30? O zinco, certo? Então:

68 29 C u →   68 30 Z n + 0 - 1 e

Na letra a teremos então o 68 30 Z n como núcleo – filho e um decaimento β - .

Passo 2

Na letra b, o cádimo possui:

A = 103

Z = 48

Se fizermos a razão entre ele:

A Z = 103 48 = 2,15

A = 2,15   Z

Ou seja, A > 2 Z e estamos na zona da instabilidade, abaixo da nossa banda de estabilidade. Isso significa que ele possui uma baixa proporção de nêutrons e deverá sofrer decaimento de uma partícula β + .

Como vai ficar então a reação?

103 48 C d →   A Z X + 0 + 1 e

Agora vamos olhar o valor de cada uma:

103 = A + 0 → A = 103

48 = Z + 1 → Z = 47

Qual elemento tem número atômico igual a 47? A prata, certo? Então:

103 48 C d →   103 47 A g + 0 + 1 e

Na letra a teremos então o 103 47 A g como núcleo – filho e um decaimento β + .

Passo 3

Já estão manjando tudo, né?

Na letra c, o berquélio possui:

A = 24 3

Z = 97

Se fizermos a razão entre ele:

A Z = 243 97 = 2 , 5

A = 2 , 5   Z

Ou seja, A > 2 Z e estamos na zona da instabilidade, bem próxima da região vermelha.

Normalmente, elementos com número atômico maior que 82 sofrem decaimento α .

Como vai ficar então a reação então?

24 3 97 B k →   A Z X + 4 2 α

Agora vamos olhar o valor de cada uma:

243 = A + 4 → A = 239

97 = Z + 2 → Z = 95

Qual elemento tem número atômico igual a 95? O amerício? Então:

243 97 B k →   239 97 A m + 4 2 α

Na letra a teremos então o 239 97 A m como núcleo – filho e um decaimento α .

Passo 4

Finalizando com a d, o dubnium possui:

A = 2 60

Z = 105

Se fizermos a razão entre ele:

A Z = 2 60 105 = 2 , 47

A = 2 , 47   Z

Ou seja, A > 2 Z , como Z > 82 ele sofre decaimento α .

Como vai ficar então a reação então?

260 105 D b →   A Z X + 4 2 α

Agora vamos olhar o valor de cada uma:

2 60 = A + 4 → A = 2 56

105 = Z + 2 → Z = 103

Qual elemento tem número atômico igual a 103? O senhor Laurêncio ? Então:

260 105 D b →   256 103 L r + 4 2 α

Na letra a teremos então o 256 103 L r como núcleo – filho e um decaimento α .

Shoow né?!

Resposta

  1. Decaimento: β -   |   Núcleo-Flilho: 68 30 Z n ;
  2. Decaimento: β +   |   Núcleo-Flilho: 103 47 A g ;
  3. Decaimento: α   |   Núcleo-Flilho: 239 97 A m ;
  4. Decaimento: α   |   Núcleo-Flilho: 256 103 L r   .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a energia liberada por captura de elétron no decaimento do C o 27 57 (Exemplo 43.7 na seção 43.3 ).Uma quantidade desprezível de energia é transferida como energia cinética para o átomo result
Determine o nuclídeo produzido nos seguintes decaimentos radioativos:Decaimento α do P u 94 239 .Decaimento β - do N a 11 24 .Decaimento β + do O 8 15 .
A massa atômica do C 14 é igual a 14,003242u . Mostre que o decaimento β - do C 14 é energeticamente possível e calcule a energia liberada nesse decaimento.
O decaimento α do U 238 é acompanhado de um raio γ com um comprimento de onda de 0,0248 n m . Esse decaimento se deve a uma transição de núcleo entre dois níveis de energia. Qual é a energia (em M e V
O U 238 sofre decaimento espontâneo por emissão α até T h 234 . Calcule:A energia total liberada nesse processo eA velocidade de recuo do núcleo de T h 234 . As massas atômicas são 238,050788u para o