Enunciado
Química - Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente - 5ª Edição - Peter Atkins, Loretta Jones e Leroy Laverman- Ed: 5º - Capítulo 1.1 - Ex. 36
Verifique a conclusão na parte (d) do Exercício 1.35, plotando a função de onda para e determinando o número de nodo.
Passo 1
Bom gente, pela parte (d) do Exercício 1.35 nós concluímos que:
Como
Agora vamos verificar esta conclusão desenhando o gráfico.
Já sabemos que:
Então, se substituirmos para
Como x também é dada em m:
Lançando nos dados os valores de para valores de x indo de 0 até 1:
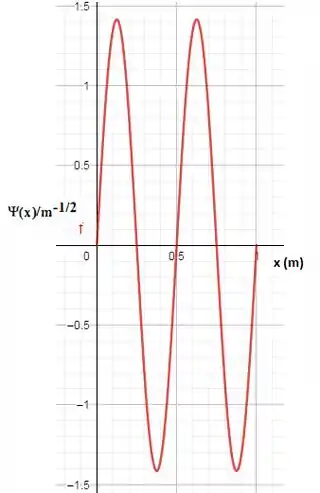
Como nós vemos pelo gráfico existem 3 nodos, ou seja, três valores de x cuja função vale zero!
Passo 2
Para achar os valores de x cuja função de onda é zero:
Aplicando o arcoseno:
Como a função se repete a cada 0,5 m, nós também teremos:
Então, para nós temos nódulo no ponto 0,25m, 0,5 m e 0,75 m, já que os demais são os extremos.
Essa foi fácil, não foi?!
Resposta
Exercícios de Livros Relacionados
(a) Qual é o fóton de mais alta energia que pode ser absorvido por um átomo de hidrogênio no estado fundamental sem causar ionização? (b) Qual é o comprimento de onda dessa radiação? (c) Em região do
(a) Use o modelo da partícula em uma caixa para o átomo de hidrogênio para tratar o elétron em uma caixa unidimensional de comprimento 150 pm e prediga o comprimento de onda da radiação emitida quando
O comprimento de onda de uma partícula em uma caixa unidimensional é dada na Eq. 9. (a) Confirme se a probabilidade de encontrar a partícula na metade esquerda da caixa é ½½, independentemente do valo
A série de Humphreys é um conjunto de linhas do espectro de emissão do átomo de hidrogênio que termina no quinto estado excitado. Se um átomo emite um fóton de radiação de comprimento de onda 5.910n m
3 – O íon Li2+ é um hidrogenóide e tem uma série de Lyman com as linhas em 740747 cm-1, 877924 cm-1, 925933 cm-1, e outras adiante. Mostre que os níveis de energia têm a forma –hcR/n2 e ache o valor d