Determinar a área, a altura e a vazão de concentrado de um sedimentador capaz de tratar de uma suspensão aquosa de barita, sabendo que se espera obter uma relação de .
Um teste de proveta, realizado à mesma concentração e temperatura de alimentação, produziu o seguinte resultado:
![]()
Passo 1
O primeiro passo que temos que fazer é pegar essa tabela de e transformá-la em um gráfico pra podermos trabalhar.
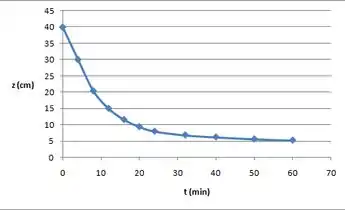
Vamos nas contas precisar de , e ; no caso do , já conseguimos determinar direto com a bissetriz nas tangentes, saca só:
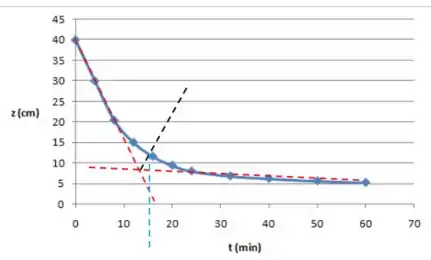
Para os outros tempos, primeiro precisamos calcular :
Do gráfico:
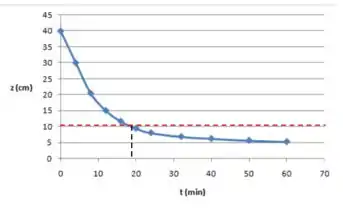
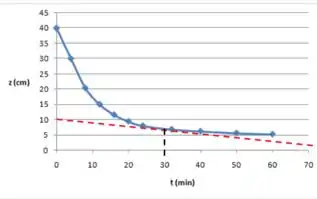
Passo 2
Para calcular a área, calculamos a área mínima e depois aplicamos os fatores de correção.
Usando o metro como unidade de comprimento, e :
Mas:
Se nada for falado, EU uso o valor médio, isto é, . Quanto a :
Em que é o diâmetro calculado a partir da .
Daí:
Então:
Passo 3
Precisamos das alturas das quatro zonas:
Para , tem as recomendações do livro do Perry:
O meu professor falava pra usarmos os valores médios desses intervalos. Daí:
Para :
Como: