Determinar o diâmetro e a altura de um sedimentador para operar com de uma suspensão aquosa de barita ( ) a . A concentração de sólidos na alimentação é de de suspensão e o lodo final deve ter de suspensão. Ensaio de proveta a conduziu ao seguinte resultado:
![]()
Passo 1
Primeiro de tudo: o enunciado deu concentrações em massa por volume , mas precisamos de concentrações volumétricas ! Daí, dividiríamos pela densidade para converter essa massa do numerador pra volume:
Escrevi isso só pra chamar sua atenção pra esse detalhe, mas na real nem vamos precisar fazer isso nessa questão porque vamos trabalhar com razão de concentrações. Espera aí que vou te mostrar isso melhor.
Antes, bora transformar esses dados de em um gráfico para podermos trabalhar:
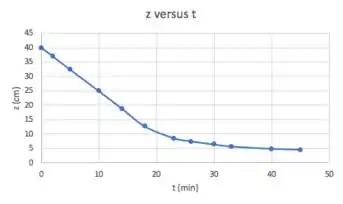
Passo 2
Bora começar com a área; para calcular a área, calculamos a área mínima e depois aplicamos os fatores de correção.
Precisamos calcular o pra poder tirar, do gráfico, .
E daí o não precisar converter as unidades de concentração pra esse problema, mas bora mostrar que a gente sabe:
Daí:
Do gráfico:
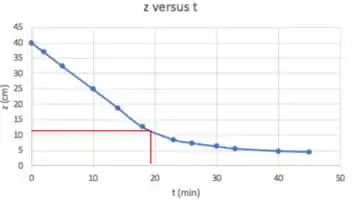
Agora já podemos calcular :
Usando metro e hora:
Mas:
Se nada for falado, EU uso o valor médio, isto é, . Quanto a :
Em que é o diâmetro calculado a partir da .
Daí:
Então:
Mas o que o enunciado pediu foi o diâmetro:
![]()
Passo 3
Precisamos das alturas das quatro zonas:
Para , tem as recomendações do livro do Perry:
O meu professor falava pra usarmos os valores médios desses intervalos. Daí:
Para :
Ainda não calculamos . Bora lá:
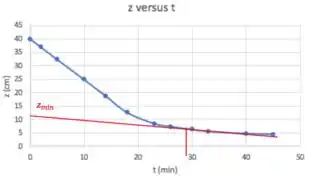
Eu li
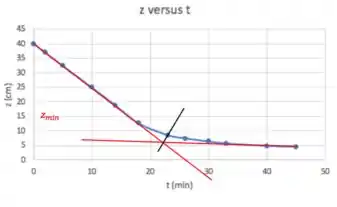
Eu li
Convertendo esses dois tempos para hora:
Daí:
Novamente, nem precisamos converter as concentrações por se tratar de uma divisão; os fatores de conversão seriam os mesmos em cima e embaixo nesse exemplo.
Como: