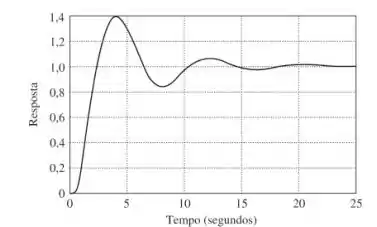
Para a resposta ao degrau unitário mostrada abaixo, obtenha a função de transferência aproximada do sistema.
Passo 1
Bora lá?
O exercício pede que gente encontre a função de transferência para a resposta que é mostrada no gráfico, para isso precisamos encontrar o ganho (), a constante de tempo (), e o fator de amortecimento ().
Passo 2
Vamos começar pelo ganho que é o mais direto.
O ganho, pela definição pode ser calculado pela variação da variável de saída (gráfico) sobre a variação da variável de entrada, que é o degrau unitário.
Passo 3
O fator de amortecimento pode ser calculado através do overshoot (). Overshoot é a razão entre o quanto o primeiro pico excede o valor do estado estacionário e a variação do estado estacionário.
Porém, existem uma fórmula que relaciona o fator de amortecimento com o overshoot:
Elevando os dois lados ao quadrado:
Passo 4
Para encontrar a constante de tempo, , podemos usar o tempo de estabilização () ou o tempo do primeiro pic0).
Você usa o que achar melhor, ou o que estiver mais fácil de visualizar no gráfico.
Usando o tempo de estabilização para uma faixa de . Podemos estimar pelo gráfico que esse tempo é atingido em aproximadamente segundos:
Estimando o tempo do primeiro pico como aproximadamente segundos:
Passo 5
O último passo é substituir tudo na função de transferência padrão: