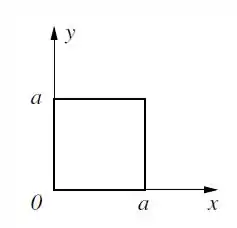
Um elétron está confinado dentro de uma caixa quadrada de lado a, mostrada na figura abaixo.

Os estados estacionários normalizados deste elétron são dados por

Onde n,m são números inteiros positivos. A energia de cada um destes estados é dada por

Onde é a massa do elétron

1. Determine a probabilidade de encontrar o elétron na região do plano , para m e n quaisquer.
2. Quais são os 4 pares de valores distintos dos números quânticos n e m correspondentes às três menores energias?
3. Quantos elétron são necessários para preencher completamente os estados com as energias calculadas no item (b)? Suponha que os elétrons não interagem entre si e leve em conta principio de exclusão de Pauli.

No item B devemos tomar cuidado com um pequeníssimo detalhe dado no enunciado. Ele nos afirma que os números quânticos são números inteiros e positivos, ou seja, não abrangem nesse caso o zero. Logo os menores estados de energias iram levar em consta os valores de

E

Como ele quer apenas os 4 pares de valores distintos que correspondem aos 3 menores níveis de energia teremos que esses pares serão

E sabemos que a energia dada nesse caso é

Substituindo os valores dos pares dos menores níveis de energia teremos os seguintes estados de energia associado

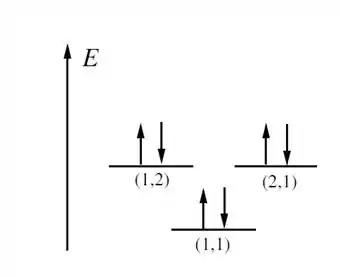
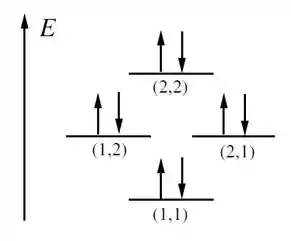
Agora para o item C basta pensar no seguinte, como os elétrons são férmions, sabemos que só podem haver 2 deles, basta lembrar que temos apenas dois spins possíveis para o elétron, que são dados pelos valores . como só temos duas posições possíveis para o elétron e nesse caso possuímos 4 estados, para preenchermos totalmente os níveis são necessários então 8 elétrons. Pela figura abaixo fica mais fácil compreender como funciona isso.

Vale lembrar também que como já calculamos no item anterior os estados (1,2) e (2,1) possuem a mesma energia.

Seguindo o passo a passo teremos o seguinte.

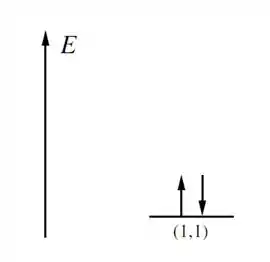
Para o estado (1,1)

Para o estado (1,2) e (2,1)

para o estado (2,2)