Usando o teorema de Thevenin, determine no circuito abaixo:
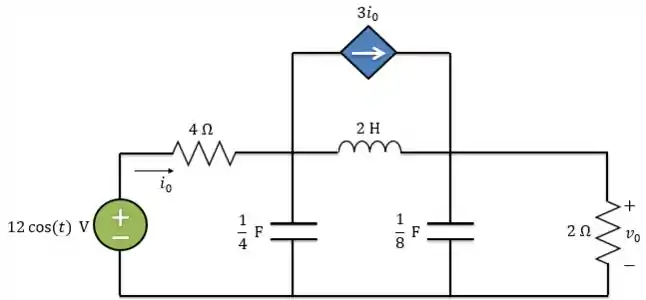
Passo 1
De cara, temos que passar o circuito para o domínio da frequência:
Portanto, o circuito no domínio da frequência será:
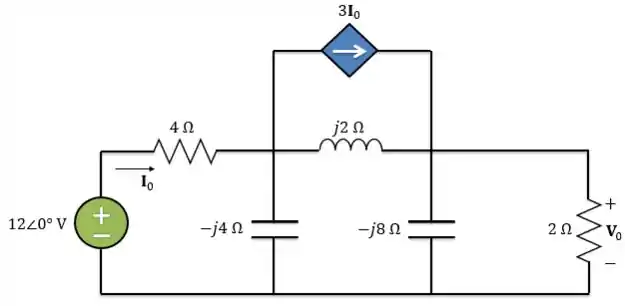
Passo 2
Agora, vamos aplicar o teorema de Thevenin para encontrar . Para isso, temos que retirar o resistor de e encontrar o circuito equivalente de Thevenin a esquerda dos terminais .
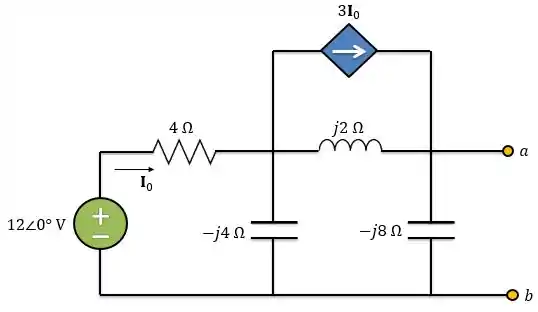
Passo 3
Agora, vamos calcular . O circuito tem uma fonte dependente de corrente, temos que lembrar que não desligamos fontes dependentes, apenas desligamos as independentes.
Além disso, para esse caso nós conectamos uma fonte de tensão nos terminais que fornece ao circuito uma corrente e encontramos através da relação abaixo:
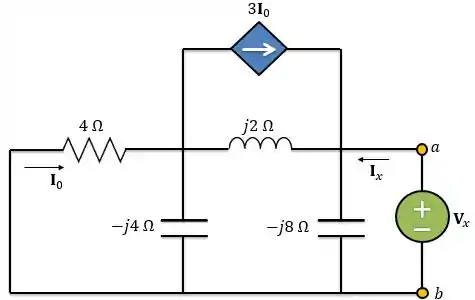
Passo 4
Para encontrar vamos utilizar análise nodal no circuito abaixo:
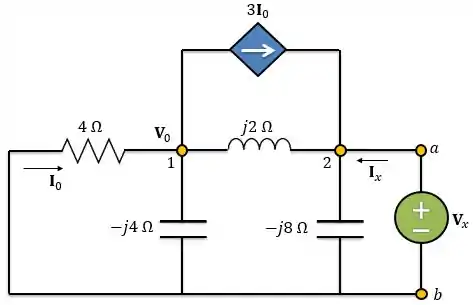
Aplicando a LCK ao nó 1:
Pela lei de Ohm:
Substituindo:
Agora, vamos aplicar a LCK ao nó 2:
Substituindo e simplificando, temos:
Passo 5
Igualando as equações e , temos:
Agora, vamos simplificar:
Portando:
Passo 6
Agora precisamos encontrar que é a tensão de circuito aberto entre os terminais .
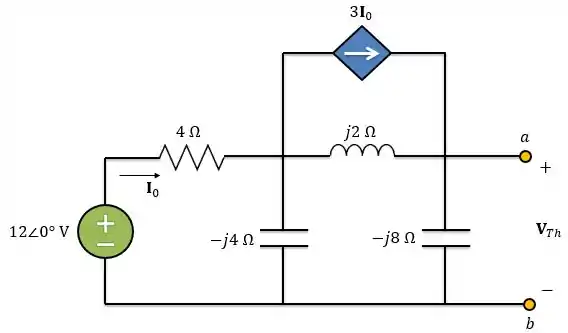
Para isso, vamos utilizar mais uma vez análise nodal.
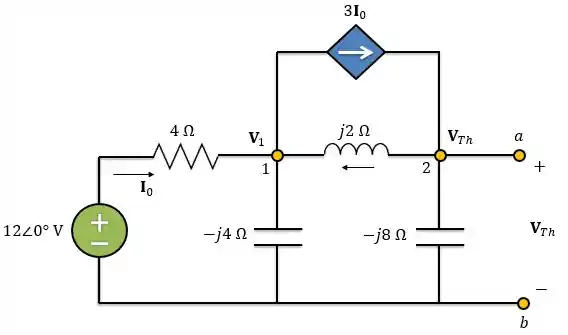
Aplicando a LCK ao nó 1:
Nesse circuito:
Substituindo:
Agora, vamos aplicar a LCK ao nó 2:
Substituindo o valor e simplificando, temos:
Passo 7
Com as equações e chegamos ao sistema abaixo:
Isolando em :
Agora, substituindo em :
Passo 8
Agora que temos os valores de e podemos substituir todo o circuito a esquerda dos terminais pelo circuito equivalente de Thevenin.
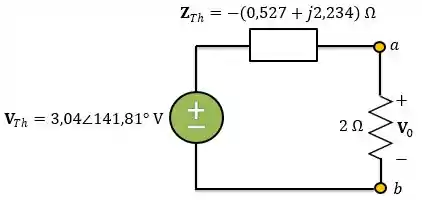
Agora, vamos aplicar divisor de tensão para encontrarmos :
Para terminar, precisamos voltar para o domínio do tempo: