Calcule a relação para um cilindro cuja altura é o dobro do diâmetro da base.
Passo 1
Primeiro de tudo, bora fazer um rascunho da geometria:
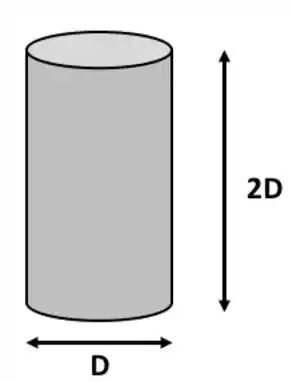
Passo 2
Vou começar calculando o e, para isso, vou precisar do volume desse cilindro aí.
Agora vamos aplicar a fórmula / definição de
:
Cortando os e isolando o :
Aplicando raiz cúbica dos dois lados:
Passo 3
Vamos agora calcular o . Para isso precisamos da área projetada do cilindro, certo?
Mas lembra que eu disse lá na teoria que pegamos sempre a maior área projetada!
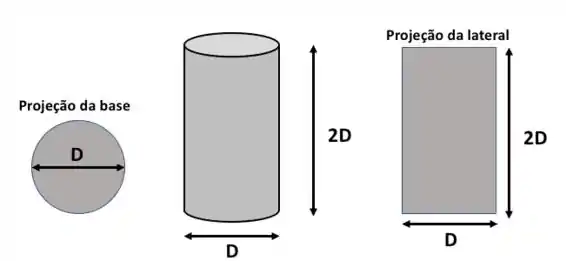
Como meu desenho tá em escala, já fica claro qual projeção é maior: projeção da lateral. Calculando as duas áreas vamos ver que é isso mesmo:
Daí vamos usar a área da projeção lateral:
Aplicando a fórmula / definição de o :
Passo 4
Agora é só dividir um pelo outro:
Cortando o “” em cima e embaixo e jogando o que sobrou na calculadora: