Para uma partícula de alumina com o formato de um paralelepípedo com dimensões proporcionais a 7x5x2:
- Calcule e
- Sabendo que esta partícula será utilizada como catalisador em uma certa reação química, qual dos dois diâmetros é o mais indicado para descrever a partícula?
Dica: Lembre que uma catálise ocorre na superfície do catalisador.
Passo 1
Como as dimensões são proporcionais a 7x5x2, se uma dimensão vale 2L, por exemplo, as outras valem 5L e 7L.
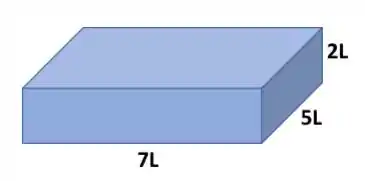
E ah, uma coisa, não faz diferença aqui se você tiver chamado a altura de 5L ou 7L ao invés do 2L, por exemplo, ok? A ordem não faz diferença.
Passo 2
Vamos, primeiro, calcular o e, para isso, precisamos do volume da partícula
Aplicando a definição de
Só um detalhe agora: esse enunciado não disse nada de unidade, né? Mas sabemos que diâmetro tem unidade de comprimento (u.c.), então, bora representar só pra evitar problema.
Passo 3
Precisamos agora calcular o , que é o diâmetro equivalente da esfera de mesma área superficial que a partícula.
A primeira coisa que vamos precisar, então, é da área superficial da nossa partícula. Como a nossa partícula é:
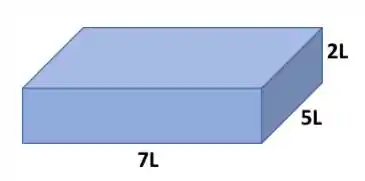
A área superficial dela vai ser:
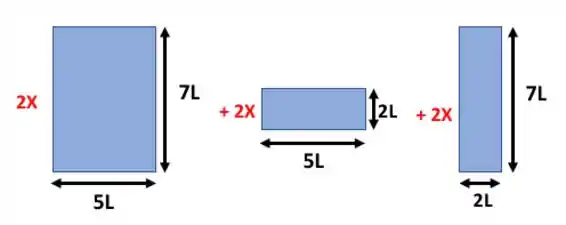
Escrevendo isso:
Aplicando agora a definição de :
Aplicando raiz quadrada dos dois lados:
Novamente, bora lembrar que diâmetro tem unidade de comprimento (u.c.), daí:
Passo 4
Agora o item b:
Sabendo que esta partícula será utilizada como catalisador em uma certa reação química, qual dos dois diâmetros é o mais indicado para descrever a partícula?
O enunciado diz que a partícula vai ser usada como catalisador e que catálises ocorrem na superfície do catalisador.
Daí, o diâmetro mais indicado é o , pois se relaciona com a área superficial da partícula e é isso que importa para nossa aplicação.
O que adianta sabermos o volume exato da partícula se o que importa para a gente é a área superficial?

Na teoria vimos 5 formas de comparar nossas partículas com esferas semelhantes, certo? Mas quando usa cada uma delas?
O ideal seria analisar a aplicação da partícula e ver o qual a propriedade se relaciona com aquela aplicação. Mas acaba que, na prática, muitas vezes usa-se o porque é mais fácil de medir experimentalmente.
Resposta
a)
b), pois é baseado na propriedade relacionada com a aplicação da partícula, área superficial, no caso.