Se em um gerador trifásico conectado em estrela equilibrado, determine as tensões de fase supondo que a sequência de fases seja:
Passo 1
A conexão estrela de um circuito trifásico é representada abaixo:
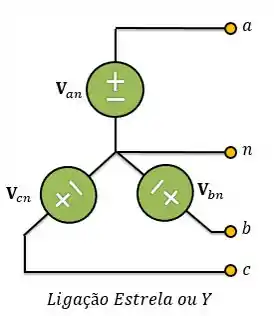
O enunciado fornece o valor da tensão de linha e diz que o circuito é equilibrado. Logo, o módulo das tensões de linha e serão iguais ao módulo da tensão de linha que foi fornecida, . Então:
Passo 2
Agora precisamos analisar para descobrir os ângulos das tensões de linha. Considerando que esteja na referência e adotando sequência como foi pedido na letra a):
Passo 3
Beleza! Estamos quase lá! Já temos módulo e ângulo de todas as tensões de linha. Só que o enunciado pede as tensões de fase. E agora?
Agora temos que lembrar da relação entre as tensões de linha e de fase em um circuito trifásico ligado em estrela:
Primeiro, vamos calcular o módulo de cada tensão de fase do circuito em estrela:
Passo 4
Agora precisamos analisar os ângulos de cada tensão de fase. Está lembrado o que modifica no ângulo quando passamos da tensão de linha para a tensão de fase na sequência ? Então... A gente tem que subtrair em cada ângulo de fase:
Prontinho!
Passo 5
Para a letra b), o que muda é que a sequência é e isso vai influenciar no ângulo das tensões. Então:
Passo 6
Da mesma forma, precisaremos calcular as tensões de fase. O módulo de cada uma delas será igual:
Passo 7
Por último, temos que analisar o ângulo das tensões de fase. Temos que tomar cuidado porque ao invés de subtrair , teremos que somar, como veremos abaixo.
Supondo que as tensões de fase sejam:
Como:
Passando para a forma polar, teremos que:
Ou seja: para a sequência , a relação entre tensão de linha e tensão de fase será:
Logo, para o nosso exercício:
Para :
Para :