102. Um gás ideal a e entra em um compressor em regime permanente. O gás é comprimido até , e da massa que entrou no compressor são removidos para alguma outra finalidade. Os restantes do gás de entrada são comprimidos a antes de sair do compressor. Todo o processo de compressão é considerado reversível e adiabático. A potência fornecida ao compressor é medida em . Considerando que o gás ideal possui calores específicos constantes, de modo que e , (a) represente graficamente o processo de compressão em um diagrama T-s, (b) determine a temperatura do gás nas duas saídas do compressor em K e (c) determine o fluxo de massa na entrada do compressor em .
Passo 1
Bora fazer mais uma questãozinha sobre entropia!
Olha só! O nosso gás ideal entra no compressor em regime permanente. Sendo assim, o processo ocorre em um fluxo constante... Não há variações significativas com o tempo.
E como noss gás é um gás ideal, então ele tem a seguintes propriedades para o calor específico...
Feito isso, bora aproveitar e calcular a relação da calor específico pro gás...
Passo 2
a) Saindo dessa parte introdutória, vamos logo por que interessa e fazer o que pede a questão nessa letra. Isto é, representat o processor em um diagrama .
Para isso, vamos considerar três situações. Chamaremos de o instante inicial em que o gás está prestes a entrar no compressor, de refere-se ao instante em que o gás foi comprimido até , sendo uma parte de dele removida e refere-se à compressão do gás até .
Dito isso, aqui está o nosso gráfico...
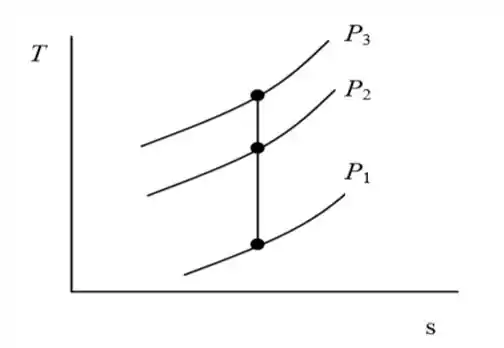
Passo 3
b) Bom! Vamos representar essas pressões da figura acima, de outro modo pra facilitar nossa compreensão...
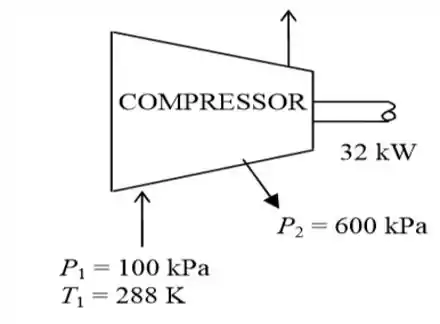
E em seguida, bora obter o valor das temperaturas e usando as equações abaixo...
Como já sabemos o valor de e das outras variáveis dessas duas equações pela figura anterior, então bora pro cálculo...
E obtemos assim, que:
Passo 4
c) Antes de ir pra análise energética, bora dar uma analisada na massa que sai e entra do nosso sistema.
Olha só! Uma parte do gás, o equivalente a , sai do nosso sistema de análise depois que o gás foi comprimido até , no processo que chamamos de . Sendo assim, o fluxo de massa na entrada, em , é igual ao fluxo de massa em somado com o fluxo de massa em , na saída e final da compressão em ...
Sendo assim, temos que...
Onde...
Agora, bora partir pra análise de energia de fato.
Bom! Já conhecemos a seguinte relação:
E como o gás entra em regime permanente no compressor, além do fato que o enunciado nos diz que todo o processo é reversível e adiabático, então...
Além disso, sabemos do fato que uma potência de foi fornecido ao compressor. Desse modo, nossa relação passa a ter a seguinte cara...
Os efeitos de energia cinética e potencial aqui são desprezíveis, tá!? Foi mal se não foi avisado!
Isolando ...
E sabendo que , e podem ser escritas como...
Basta fazer a troca na equação anterior e substituir os valores numéricos, alguns dos quais, já obtemos no :
Pronto! Obtemos o fluxo de massa na entrada!
Resposta
a)
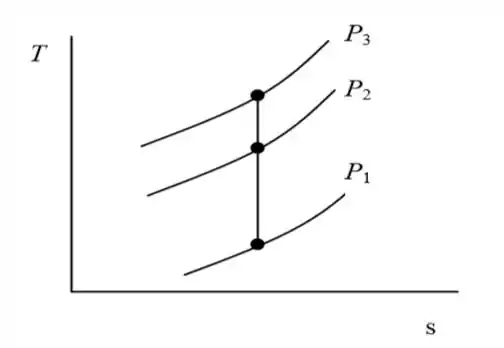
b)
c)