Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 22

Um aquecedor de água fechado aquece 20   k g / s de água de 100   ° C e 20   M P a até 250   ° C e 250   M P a em um ciclo de potência de vapor regenerativo, conforme mostrado na Fig. P11.22. O vapor extraído da turbina entra no aquecedor a 4   M P a e 275   ° C e sai como líquido saturado. Qual é a vazão mássica da extração de vapor?

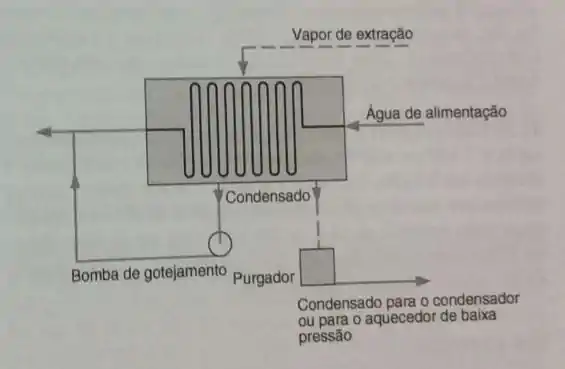
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Nós temos os seguintes dados, para este caso

m 2 ' = 20 k g s

t 2 = 100   ° C

p 2 = p 3 = 20   M P a

t 3 = 250   ° C

p 6 = 4   M P a

t 6 = 275   ° C

Nós estamos assumindo que Q = 0 . Também temos que as perdas potenciais e cinéticas são desprezadas e o trabalho da bomba pode ser desprezado, logo,

w b o m b a = 0

Passo 2

A tarefa é determinar a vazão de massa necessária do vapor de extração.

A diferença do aquecedor OFW é que no aquecedor CFW não há contrato direto entre os fluidos, portanto não há mistura entre eles. Vamos determinar a entalpia para os estados:

O estado (6) é determinado pela tabela B.1.3, com os valores correspondentes a p 6 = 4000   k P a e t 6 = 275   ° C usando a interpolação linear. Com isso,

t ' = 250   ° C → h ' = 2801,38 k J k g

t ' ' = 300   ° C → h ' ' = 2960,68 k J k g

Calculando a entalpia com interpolação linear:

h 6 - h ' h ' ' - h ' = t 6 - h ' t ' ' - t '

Desenvolvendo a igualdade e isolando o h 6

h 6 = t 6 - t ' t ' ' - t ' ∙ h ' ' - h ' + h '

Substituindo os termos

h 6 = 275 - 250 300 - 250 ∙ 2960,68 - 2801,38 + 2801,38 = 2881,03 k J k g

O estado (6a) é determinado por p 6 = 4000   k P a em linha vapor saturado de água ou qualidade x da mistura, que é fornecido pela tabela B.1.2

h 6 a = h f   p a r a   4000   k P a = 762,79 k J k g

Para o estado (2), nós conseguiremos através da tabela B.1.4, com valores correspondentes a p 2 = 20   M P a e t 2 = 100   ° C

h 2 = 434,04 k J k g

Passo 3

O estado (3) é determinado pela tabela B.1.4, tomamos a entalpia entre nossos parâmetros de pressão e temperatura, com valores correspondentes a p 3 = 20000   k P a e t = 250 ° C

t ' = 240   ° C → h ' = 1040,04 k J k g

t ' ' = 2 6 0   ° C → h ' ' = 1 133 , 4 5 k J k g

Calculando a entalpia com interpolação linear:

h 3 - h ' h ' ' - h ' = t 3 - h ' t ' ' - t '

Desenvolvendo os termos

h 6 = t 6 - t ' t ' ' - t ' ∙ h ' ' - h ' + h '

Substituindo os termos

h 6 = 250 - 240 260 - 240 ∙ 1133,45 - 1040,04 + 1040,04

Portanto,

h 6 = 1086,74 k J k g

Passo 4

A equação de energia para aquecedor sem transferência externa de calor e sem trabalho:

E n e r g i a i n t e r n a = E n e r g i a s a í d a

Nosso problema tem 2 entradas e 2 saídas. Então, a equação de energia é dada por:

m 2 ' ∙ h 2 + m 6 ' ∙ h 6 = m 2 ' ∙ h 3 + m 6 ' ∙ h 6 a

Agora podemos calcular o fluxo de massa necessário do vapor de extração:

m 6 ' = m 2 ' ∙ h 3 - h 2 h 6 - h 6 a

Substituindo os termos

m 6 ' = 20 ∙ 1086,74 - 434,04 2881,03 - 762,79 = 6,162 k g s

Resposta

m 6 ' = 6,162 k g s

Exercícios de Livros Relacionados

Uma planta de potência a vapor, operando em um ciclo ideal de Rankine, tem uma pressão alta de 5 Mpa e uma pressão baixa de 15 kPa. O estado da exaustão da turbina deve apresentar um título de pelo me
Uma usina termelétrica simples a vapor apresenta, supostamente, os quatro estados listados a seguir: 1: (20°C, 100 kPa), 2: (25°C, 1 MPa), 3: (1000°C, 1 MPa), 4: (250°C, 100 kPa), com uma fonte de ene
Considere um ciclo ideal de vapor com reaquecimento, conforme mostrado na Fig. P11.15, onde o vapor entra na turbina de alta pressão a 3M P a e 400° C e é expandido para 0,8M P a . Em seguida, o vapor
Um aquecedor de água aberto, em um ciclo de potência de vapor regenerativo, recebe 20k g / s de água a 100° C e 2M P a . O vapor extraído da turbina entra no aquecedor a 2M P a e 275° C , e toda a águ
Vapor entra na turbina de uma usina a vapor a 5M P a e 400° C e sai para o condensador a 10k P a . A turbina produz 20000k W de potência com um rendimento isoentrópico de 85 % . Qual é a vazão mássica