Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 39

Um arranjo pistão-cilindro contém vapor de água inicialmente a 200 kPa, 200 °C e 0,4 m 3 . Nesse estado, uma mola linear ( F   α   x ) está tocando o pistão, mas sem exercer qualquer força sobre ele. Calor é então transferido lentamente para o vapor, fazendo com que a pressão e o volume sejam elevados para 250 kPa e 0,6 m 3 , respectivamente. Mostre o processo em um diagrama P - V que inclua as linhas de saturação e determine (a) a temperatura final, (b) o trabalho realizado pelo vapor e (c) o calor total transferido.

Passo 1

Temos que as propriedades do vapor de água podem ser retiradas da tabela de vapor, assim, temos:

Para as condições iniciais de T 1 = 200   ° C ,   P 1 = 200   k P a , temos:

υ 1 = 1,08049   m 3 / k g

u 1 = 2654,6   k J / k g

Daí, conseguimos descobrir a massa do vapor de água, que não se alterará durante o processo, assim:

m = V 1 υ 1 = 0,4   m 3 1,08049   m 3 / k g = 0,37   k g

Como a massa do vapor não irá se alterar e temos o volume final, conseguiremos encontrar o volume específico final do vapor, e como temos a pressão final, conseguiremos encontrar a que temperatura o vapor se encontra, assim:

υ 2 = V 2 m = 0,6   m 3 0,37   k g = 1,6216   m 3 / k g

Buscando por P 2 = 250   k P a e υ 2 = 1,6216   m 3 / k g na tabela de vapor veremos que precisaremos fazer uma interpolação para encontrar o valor desejado. Interpolando encontramos a seguinte temperatura final de T 2 = 606   ° C e energia interna de u 2 = 3312   k J / k g .

Passo 2

Ao consultar as tabelas verificamos que o vapor está superaquecido, então teremos nosso diagrama P - V da seguinte forma:

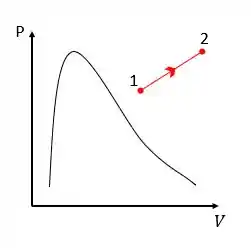
Passo 3

O trabalho será dado pela área sob a curva do processo no diagrama P - V , observe que temos um trapezoide abaixo da curva, portanto, o trabalho pode ser dado por:

W = á r e a   s o b   a   c u r v a = P 1 + P 2 2 ( V 2 - V 1 )

W = 200 + 250 k P a 2 0,6 - 0,4 m 3 = 45   k P a ⋅ m 3 = 45   k J / k g

Passo 4

Temos que nosso balanço de energia pode ser dado por:

Δ U + E C + E P s i s t e m a = Q + W - Δ H + E C + E P c o r r e n t e s

Adotando o arranjo cilindro-pistão, vamos ter as seguintes considerações:

  • Não temos correntes, sistema fechado, Δ H + E C + E P c o r r e n t e s = 0 ;
  • As energias potencial e cinética podem ser desprezadas, Δ E C + E P s i s t e m a = 0 ;

Assim, nosso balanço fica da seguinte forma:

Δ U ^ - W = Q

Assim, o calor transferido será dado por:

Q = 0,37   k g × 3312   k J / k g - 2654,6   k J / k g - - 45   k J / k g = 288   k J

Note que o trabalho “entra” negativo no balanço por questão de referencial, temos que o trabalho está sendo realizado do sistema para suas vizinhanças.

Resposta

Assim,

  1. 606 °C;
  2. 45 kJ;
  3. 288 kJ.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um conjunto cilindro-pistão nitrogênio. Inicialmente, o nitrogênio apresenta pressão e temperatura iguais a 1500k P a e 750K . O gás é então expandido, num processo politrópico com n = 1,2 , até que a
Um conjunto cilindro-pistão contém 0,1k g de ar. Inicialmente, a pressão e a temperatura do ar são iguais a 100k P a e 300K . O ar é então comprimido, lenta e isotermicamente, até que a pressão atinja
A câmara de combustão de um automóvel, mostrada na Fig. P5.107, contém inicialmente 0,2L de ar a 90k P a e 20 ° C . O ar é, então, comprimido num processo politrópico quase-estático, com expoente n =
Um guindaste levanta uma carga de 450k g verticalmente. Sabendo que a potência utilizada nesta movimento é 1k W , determine a velocidade de ascensão da carga.
Determine a transferência de calor no processo descrito no Prob.4.55.