Um gás ideal passa por dois processos em um arranjo pistão-cilindro, da seguinte maneira:
Compressão politrópica de e com o expoente politrópico n e a razão de compressão de .
Expansão a uma pressão constante a até .
- Esboce o processo em um único diagrama .
- Obtenha uma expressão para a razão do trabalho de compressão-expansão como uma função de n e r.
- Encontre o valor dessa razão para valores de e .
Passo 1
O processo no diagrama é dado da seguinte forma:
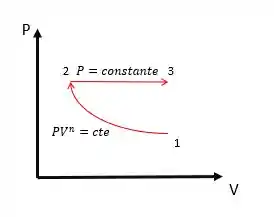
Passo 2
Temos que a expressão para calcular o trabalho vem da seguinte integral:
Para a compressão politrópica, teremos que a pressão não será constante, daí, substituiremos P na integral, assim:
Do processo de expansão, teremos a pressão constante, daí, o trabalho será dado por:
Note que, pela expressão de uma compressão politrópico conseguimos chegar na seguinte relação de volume e temperatura:
Temos que , daí:
Já na expansão a pressão constante, teremos , e , assim:
Queremos encontrar uma expressão para o trabalho de compressão-expansão como função de , assim, fazendo a razão dos dois trabalhos, temos:
Colocando as temperaturas em termos de , temos:
Passo 3
Considerando e , teremos substituindo na expressão de razão dos trabalhos compressão-expansão o seguinte valor:
Resposta
Assim,
(b)
(c) 0,256.