Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 149
Um compressor de ar comprime de ar a 120 kPa e 20 °C para 800 kPa e 300 °C enquanto consome 6,2 kW de potência. Quanto dessa potência está sendo utilizada para aumentar a pressão do ar, e qual é a potência necessária para mover o fluido pelo compressor?
Passo 1
Vamos desenhar um esquema:
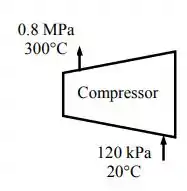
O fluxo é constante e o ar é um gás ideal. A constante do ar é
Então, o volume específico do ar na entrada é:
O fluxo de massa do ar é:
Comparando o fluxo de trabalho com a equação dos gases ideais:
Passo 2
Então, teremos:
Potência que está sendo utilizada para aumentar a pressão do ar:
Potência necessária para mover o fluido pelo compressor:
Resposta
Exercícios de Livros Relacionados
Vapor de água é comprimido por um compressor adiabático de 0,2 MPa e 150 °C até 0,8 MPa e 350 °C a uma taxa de 1,30 kg/s. O consumo de potência pelo compressor é de: (a) 511 kW (b) 393 kW (c) 302 kW (
Um ventilador deve acelerar ar parado até a velocidade de 8 m/s a uma taxa de 9 m 3 / s . Determine a potência mínima que deve ser fornecida ao ventilador. Suponha que a densidade do ar seja de 1,18 k
Considere um ventilador localizado em um duto quadrado de 3 pés× 3 pés. Velocidades em vários pontos na saída são medidas e velocidade do fluxo médio é determinada em 22 pés/s. Tomando a densidade do
A força motriz para o escoamento de fluidos é a diferença de pressão, e uma bomba opera elevando a pressão de um fluido (convertendo o trabalho mecânico de eixo em energia de escoamento). O consumo de
Um ventilador deve acelerar o ar parado até a velocidade de 12 m/s a uma taxa de 3 m 3 / s . Considerando que a densidade do ar é de 1,15 kg/ m 3 , a potência mínima que deve ser fornecida ao ventilad