Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 69

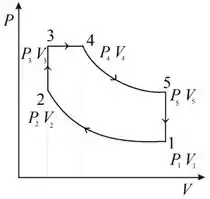
Um ciclo de ar-padrão, chamado de ciclo duplo, com calores específicos constantes, é executado em um sistema pistão- -cilindro fechado e composto dos cinco processos seguintes:

1-2 Compressão isentrópica com uma razão de compressão r = V 1 / V 2

2-3 Fornecimento de calor a um volume constante com uma razão de pressão r p = P 3 P 2

3-4 Fornecimento de calor a uma pressão constante com uma razão entre volumes r c = V 4 / V 3

4-5 Expansão isentrópica até V 5 = V 1 enquanto o trabalho é realizado

5-1 Rejeição de calor a um volume constante de volta ao estado inicial

(a) Represente graficamente os diagramas P - v   e   T - s para o ciclo.

(b) Obtenha uma expressão para a eficiência térmica do ciclo como uma função de k ,   r ,   r c   e   r p .

(c) Avalie o limite da eficiência quando r p se aproxima do valor unitário e compare sua resposta com a expressão para a eficiência do ciclo Diesel.

(d) Avalie o limite da eficiência quando r c se aproxima do valor unitário e compare sua resposta com a expressão para a eficiência do ciclo Otto.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Abaixo estão representados os diagramas P - v   e   T - s para o ciclo:

A eficiência de qualquer ciclo é dada por:

η = 1 - q s a i q e n t

Desenvolvendo, temos que:

η = 1 - c v T 5 - T 1 c v T 3 - T 2 + c p T 4 - T 3

Sabendo que:

k = c p c v

Temos que:

η = 1 - T 5 - T 1 T 3 - T 2 + k T 4 - T 3

η = 1 - T 1 T 5 T 1 - 1 T 2 T 3 T 2 - 1 + k T 3 T 4 T 3 - 1

η = 1 - T 1 T 2 T 5 T 1 - 1 T 3 T 2 - 1 + k T 3 T 2 T 4 T 3 - 1

Passo 2

Analisando as relações de temperatura, temos que:

T 1 T 2 = 1 r k - 1

T 3 T 2 = r p

E:

T 4 T 3 = r c

Portanto:

T 5 T 1 = T 5 T 4 ⋅ T 4 T 1

T 5 T 1 = v 4 v 5 k - 1 ⋅ T 4 T 3 ⋅ T 3 T 1

Substituindo a razão de corte, temos que:

T 5 T 1 = v 4 v 5 k - 1 ⋅ r c ⋅ T 3 T 2 ⋅ T 2 T 1

T 5 T 1 = v 4 v 5 ⋅ v 1 v 2 k - 1 ⋅ r c ⋅ r p

T 5 T 1 = r c k - 1 ⋅ r c ⋅ r p

Logo:

T 5 T 1 = r c k ⋅ r p

Passo 3

Substituindo os valores de temperatura na expressão da eficiência, temos que:

η = 1 - T 1 T 2 T 5 T 1 - 1 T 3 T 2 - 1 + k T 3 T 2 T 4 T 3 - 1

Simplificando, temos que:

η = 1 - 1 r k - 1 r c k r p - 1 r p - 1 + k r p r c - 1

Passo 4

Aplicando o limite de eficiência, pois a razão de pressão tende à unidade, temos que:

lim r p → 1 ⁡ η = lim r p → 1 ⁡ 1 - 1 r k - 1 r c k r p - 1 r p - 1 + k r p r c - 1

lim r p → 1 ⁡ η = 1 - r c k - 1 r k - 1 k r c - 1

Aplicando o limite de eficiência com a razão de corte tendendo a unidade, temos que:

lim r c → 1 ⁡ η = lim r c → 1 ⁡ 1 - 1 r k - 1 r c k r p - 1 r p - 1 + k r p r c - 1

lim r c → 1 ⁡ η = 1 - r p - 1 r k - 1 r P - 1

Logo:

lim r c → 1 ⁡ η = 1 - 1 r k - 1

Resposta

b )   η = 1 - 1 r k - 1 r c k r p - 1 r p - 1 + k r p r c - 1

c ) lim r p → 1 ⁡ η = 1 - r c k - 1 r k - 1 k r c - 1  

d ) lim r c → 1 ⁡ η = 1 - 1 r k - 1  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ciclo Diesel ideal tem uma razão de compressão de 20 e uma razão de corte de 1,3 . Determine a temperatura máxima do ar e a taxa de fornecimento de calor para esse ciclo quando se produz 250k W de
Repita o P r o b .9 - 53 , considerando que no início da compressão o ar está a 80k P a e - 20 ° C .
Desenvolva uma expressão para a razão de corte r c , expressa por q i n / ( c p T 1 r k - 1 ) , considerando um ciclo Diesel padrão a ar.
Como se pode mudar r p no P r o b .9 – 67 de modo que a eficiência térmica seja mantida mesmo quando a razão de compressão é reduzida?
Repita o P r o b .9 – 55 E considerando calores específicos constantes à temperatura ambiente.