Um cilindro com isolamento térmico é dividido em dois compartimentos, com cada, por um pistão inicialmente preso por um pino, conforme mostrado na Fig. P5.72. O compartimento tem ar a e , e o compartimento tem ar a e . O pistão é então liberado, podendo mover-se livremente, e calor é conduzido através dele de modo que o ar atinge uma temperatura uniforme . Determine a massa nos dois compartimentos e , e a temperatura e a pressão finais.
Passo 1
Fala, galera! Nessa questão nós temos um cilindro com ar, com isolamento térmico, dividido em dois compartimentos, nesse estado:
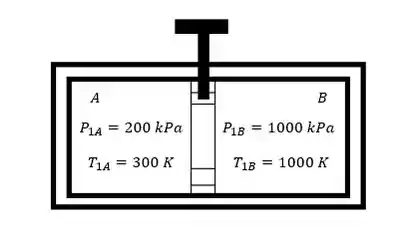
Depois que o pistão é liberado, entra calor no sistema e ele atinge uma temperatura uniforme . Quando isso acontece, nós temos que determinar a massa, a temperatura e a pressão finais. Vamos lá!
Passo 2
Para encontrar as massas, vamos usar a equação geral dos gases:
Isolando a massa , no compartimento temos:
E no compartimento :
O volume é o mesmo nos dois compartimentos . E as pressões e temperaturas em cada compartimento são aquelas na figura do passo 1, que o enunciado nos deu. Substituindo todos esses dados, temos as massas:
E
Passo 3
O cilindro tem isolamento térmico e não tem mudança de volume, isso significa que o calor transferido é zero, , e o trabalho também é zero, . Então, a primeira Lei da Termodinâmica pode ser escrita assim:
Somando os dois compartimentos, temos:
Isolando
As energias internas para o estado inicial em A e B podem ser encontradas na Tabela A.7:
Então é só substituir os dados:
Com esse resultado, nós podemos olhar de novo na Tabela A.7 para a achar a temperatura final. Interpolando, temos:
Passo 4
Para achar a pressão final, vamos usar a lei dos gases ideais novamente:
Isolando ,
Substituindo os valores:
É isso, galera, encerramos o exercício 😉.