Um cilindro ocupado com um embolo móvel contém um gás ideal a pressão , volume especifico e temperatura . A pressão e o volumem são simultaneamente aumentados, de modo que, em cada instante, e são relacionados pela equação
Onde é uma constante. (a) Expresse a constante em termos da pressão , a temperatura e a constante dos gases . (b) Faça o gráfico que representa o processo acima no plano (c) Encontre a temperatura, quando o volume especifico for dobrado, se
Passo 1
(a)
Da equação vamos isolar , então temos:
Substituindo nossos valores do enunciado,
(1)
Para deixar a resposta em termos só de e , usamos a equação dos gases ideais:
Com nossos dados, seria:
Isolando
Substituindo na equação (1)
Passo 2
(b)
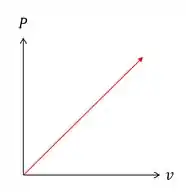
Passo 3
(c) Calculando se e
Usando novamente a equação dos gases ideais:
Multiplicando os dois lados da igualdade por
Lembrando que é definida pela equação dos gases ideais como:
Substituindo,
Isolando e substituindo os dados iniciais do problema
Usando o fato que
Substituindo
Resposta
Finalmente temos que é em termos de e é dado por e