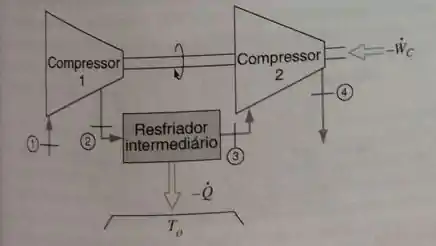
Um compressor de duplo estágio, com um resfriador entre os estágios (intercooler), recebe ar a e e comprime esse ar até , como mostrado na Fig. P9.21. O ar passa então pelo resfriador e sai a , após o que ele entra no segundo estágio, que tem uma pressão de saída de . Ambos os estágios são adiabáticos e reversíveis. Determine a transferência de calor por unidade de massa no resfriador e o trabalho específico total. Compare este resultado com o trabalho que seria requerido caso não existisse o resfriador.

Primeiro, precisamos obter dados para capacidade de calor específico e fator de expansão isentrópico da tabela A.5:

Como o processo de 1-2 é adiabático, podemos usar a seguinte equação para calcular a temperatura no estado 2:

Fazendo o processo de substituição

Agora podemos calcular o trabalho específico do primeiro compressor:

Novamente, substituindo os termos

A transferência de calor específica no intercooler é calculada a partir de:

Substituindo...

O processo 3-4 também é adiabático e usaremos a mesma equação de antes para calcular a temperatura no estado 4:

O trabalho específico do segundo compressor é igual a

Substituindo os valores

Finalmente, o trabalho específico total é:

Novamente, fazendo a substituição

A temperatura na saída se não houver intercooler será calculada também pelo fato de se tratar de um processo adiabático reversível:

Substituindo os termos

O trabalho específico se não houver intercooler será calculado a partir de:

Com isso,