Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 11.Problemas - Ex. 116

Um condicionador de ar opera no ciclo de refrigeração por compressão de vapor utilizando refrigerante-134a como fluido refrigerante. O condicionador de ar é utilizado para manter um espaço a 21 °C enquanto rejeita o calor para o ar ambiente a 37 °C. O refrigerante entra no compressor a 180 kPa superaquecido em 2,7 °C a uma taxa de 0,06 kg/s, saindo do compressor a 1.200 kPa e 60 °C. Refrigerante-134a é sub-resfriado em 6,3 °C na saída do condensador. Determine (a) a taxa de resfriamento fornecida para o espaço, em Btu/h, e o COP; (b) a eficiência isentrópica e a eficiência da exergia do compressor; (c) a destruição de exergia em cada um dos componentes do ciclo e a destruição total da exergia no ciclo, e (d) a potência mínima entregue e a eficiência de segunda lei do ciclo.

Passo 1

Oi pessoal, tudo bem?

Bem, para o problema, podemos esboçar o diagrama T-s como:

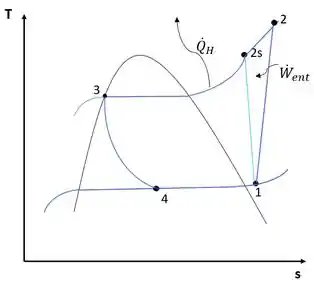
Passo 2

Assim, sabemos que o estado 1 encontrava-se em vapor saturado e foi superaquecido em . Para a saturação em a temperatura era de , com o superaquecimento tornou-se e , ou seja para o refrigerante R-134a, da tabela termodinâmica de vapor superaquecido:

Sabe-se que o estado 2 se encontra em vapor superaquecido com e que , então: .

Como , é possível descobrir também a entalpia em 2:

Assim como no estado 1, estado 3 se encontra-se em líquido saturado com , a temperatura de saturação era de aproximadamente , porém sofreu um sub-resfriamento de , ficando portanto , então:

E assumindo que há estrangulamento de 3-4, temos

A taxa de resfriamento é:

Sabendo que o COP pode ser representado por:

Passo 3

Para a letra b):

Para calcular a eficiência isentrópica do compressor:

A potência reversível e a eficiência de exergia do compressor são:

Sendo a temperatura do ambiente.

Portanto:

Passo 4

Para a letra c) a destruição de exergia em cada um dos componentes do ciclo e a destruição total da exergia no ciclo:

Para o compressor:

Então:

Para o condensador:

Então:

Para a válvula de expansão:

Então:

3−4

Para o evaporador:

Então:

3−4

Portanto a destruição total da exergia no ciclo é:

Passo 5

Para a letra d) a potência mínima entregue e a eficiência de segunda lei do ciclo:

A potência mínima pode ser representada:

E

Portanto:

E a eficiência da segunda lei:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura P 11.122 mostra o esboço de um refrigerador, que opera com R - 22 , e é acionado por um motor térmico que utiliza gás natural como combustível. O rendimento térmico do motor é igual a 25 % .

A vazão de refrigerante R - 12 , num ciclo real de refrigeração, é 0.05k g / s . O vapor entra no compressor a 150k P a e - 10 ° C e sai dele a 1.2M P a e 75 ° C . A potência consumida no compressor f

Nós não apresentamos a equação para o coeficiente de eficácia do ciclo de refrigeração a ar no texto. Derive a expressão para o coeficiente de eficácia, em função da relação de compressão do ciclo, co

Deseja-se comparar o desempenho de um refrigerador, com ciclo de absorção de amônia, com um refrigerador similar baseado no ciclo de compressão de vapor. Considere um sistema de absorção que apresenta

Um ciclo de potência a vapor deve operar com uma pressão máxima de 3M P a , pressão mínima de 10k P a e temperatura na seção de saída da caldeira a 500° C . A fonte quente disponível são 175k g / s de