Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 39

Um conjunto cilindro-pistão-mola linear contém ar. O arranjo deste conjunto é similar ao mostrado na Fig. P3.101. Nestas condições, a relação entre pressão no ar contida no conjunto e o volume de ar é dada por p = A + B V . Inicialmente, a pressão no ar é 150   k P a e o volume de ar no conjunto é 1 litro. Transfere-se calor ao ar até que a pressão atinja 800   k P a . Sabendo que o volume de ar no estado final é 1,5   litros, determine o trabalho envolvido neste processo.

Passo 1

Fala pessoal, beleza?

Galera seguinte, vamos ilustrar a situação:

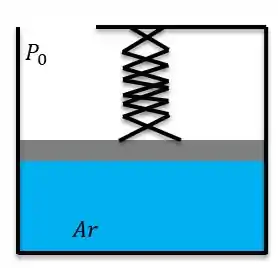
Sabendo que equação de pressão do processo é:

P = A + B V

Por uma variação linear, devido à mola, da pressão pelo volume, temos que a linha do diagrama P - V é fixo por dois pontos:

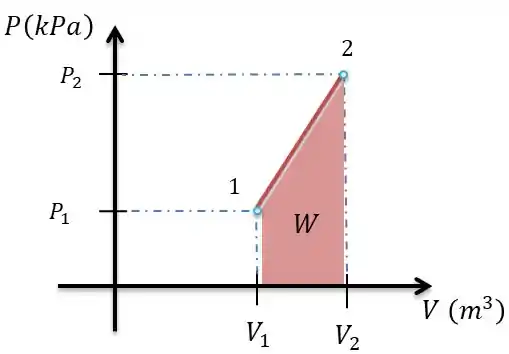
Portanto, o trabalho vai ser a integral P ∙ d V dessa área entre os pontos 1   e 2 .

Passo 2

Bem para cada estado temos os seguintes volumes:

Estado 1:

P 1 = 150 k P a   e   V 1 = 1 L = 1 ∙ 10 - 3 = 0,001   m 3

Estado 2:

P 1 = 800 k P a   e   V 2 = 1,5 L = 1,5 ∙ 10 - 3 = 0,0015   m 3

Passo 3

Condições de estado definidas, vamos aplicar a o cálculo da área sobe a reta:

W = ∫ P ∙ d V = A

A área de um trapézio nada mais é que a soma das duas bases dividas por 2 multiplicados por sua altura.

W = P 1 + P 2 2 ∙ V 2 - V 1 = 150 + 800 2 ∙ 0,0015 - 0,001

W = 0,2375   k J  

É isso pessoal valeu!

Resposta

W = 0,2375   k J  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o trabalho total (em kJ) produzido pelo processo isotérmico da figura abaixo, considerando que o sistema é composto de 3 kg de oxigênio.
Um arranjo pistão-cilindro sem atrito contém 2 kg de nitrogênio a 100 kPa e 300 K. O nitrogênio é então comprimido lentamente de acordo com a relação P V 1,4 = constante até atingir uma temperatura fi
Um arranjo pistão-cilindro inicialmente contém 0,07 m³ de gás nitrogênio a 130 kPa e 120 °C. O nitrogênio então se expande politropicamente para um estado de 100 kPa e 100 °C. Determine o trabalho de
Um arranjo pistão-cilindro com batentes contém inicialmente 0,3 kg de vapor de água a 1,0 MPa e 400 °C. A localização dos batentes corresponde a 60% do volume inicial. Nessas condições, começa-se a re
Qual dessas opções tem a capacidade de produzir o máximo trabalho em um sistema fechado: 1 kg de vapor a 800 kPa e 180 °C ou 1 kg de R-134a a 800 kPa e 180 °C? Considere T 0 = 25 ° CeP 0 = 100k P a .