Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 42
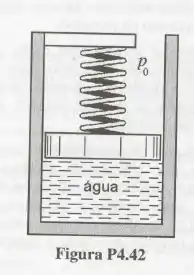
O conjunto cilindro-pistão mostrado na Fig. contém 1 de água. Inicialmente, a temperatura e a pressão na água são iguais a e . A mola é linear de modo que a pressão na água é igual a quando o volume interno do conjunto for . Transfere-se calor ao conjunto até que o volume interno se torne igual a . Determine a temperatura da água no estado final do processo, o trabalho realizado pela água e construa o diagrama referente ao processo descrito.
Passo 1
Fala pessoal, beleza?
Galera temos que calcular a temperatura final do processo e desenhar o diagrama do processo, bora lá?
Seguinte para determinar a temperatura final, iremos fazer a comparação entra as condições finais e com as tabelas e tentaremos encontrar a temperatura mais próxima.
Para o trabalho, como o nosso sistema possui uma variação de volume direta com a pressão utilizaremos fórmula do trabalho integrável:
Passo 2
Seguinte, sabemos que massa nenhuma de água vaza do sistema, portanto, temos a massa constante no processo. Sabemos o volume final o que resulta que podemos calcular o volume específico.
Com volume específico calculado e a pressão de , vamos olhar na tabela , e procurar a temperatura mais próxima:
Temos que a temperatura mais próxima da nossa condição de estado final é:
Passo 3
Devido à mola temos uma variação linear, da pressão pelo volume, temos que a linha do diagrama é fixo por dois pontos:
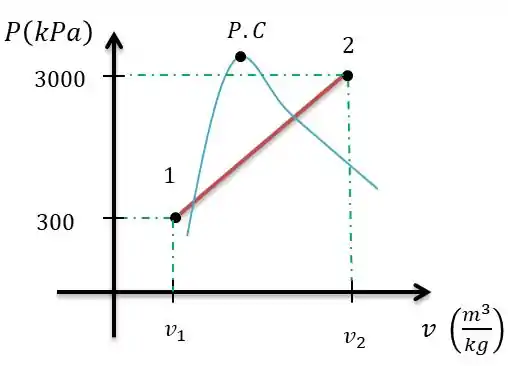
Portanto, o trabalho vai ser a integral dessa área entre os pontos e .
Como a nossa área configura um trapézio, basta calcular a área de um trapézio.
A área de um trapézio é a soma das duas bases divido por dois e multiplicados por sua altura.
Passo 4
Para encontrarmos o volume inicial, temos que utilizar a temperatura e irmos na tabela e temos:
Abrindo a fórmula do volume específico, temos:
Passo 5
Retomando o cálculo do trabalho, temos:
Resposta
Diagrama esta no passo 3.