Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 48
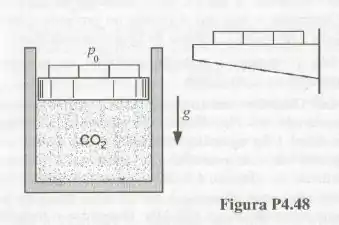
O conjunto cilindro-pistão mostrado na Fig. contém, inicialmente, de dióxido de carbono a e . Os pesos são, então, adicionados a uma velocidade tal que o gás é comprimido segundo a relação . Admitindo que a temperatura final seja a, determine o trabalho realizado neste processo.
Passo 1
Fala galera, beleza?
Temos uma relação de em que o nosso expoente é , portanto, vamos ter que utilizar a equação que foi deduzida na página 76, equação , que é o seguinte:
Basicamente temos todos os dados para calcular o trabalho menos o nosso , para eles podemos assumir que o é um gás ideal, então bora calcular o nosso .
Passo 2
Calculando .
A equação do gás ideal é definida por:
Agora nos entramos em outro problema, não temos a massa, apenas a temperatura.
A boa notícia que a massa e a constante dos gases ideias também. Estes dois itens são iguais no estado inicial e final, logo vamos aplicar equação do gás ideal no estado inicial para determinar .
Antes de substituir os dados, vamos converter a temperatura para kelvin.
Substituindo os dados em :
Substituindo na equação do , fica:
Passo 3
Com determinado e as temperaturas convertidas para Kelvin, podemos aplicar a fórmula escrita no passo 1:
Trabalho negativo isso significa que o processo esta retirando calor do sistema.