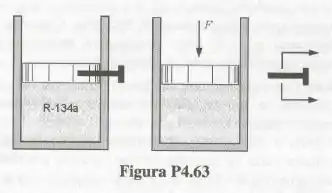
O conjunto cilindro-pistão mostrado na Fig. P.4.63 contém de refrigerante . Inicialmente , a temperatura e a pressão são iguais a e . Transfere-se calor do refrigerante até que o refrigerante atinja o estado de vapor saturado . Neste processo, o pistão se encontra travado com o pino. O pino é então removido a uma força constante é aplicada no pistão de modo a equilibra-lo. O resfriamento continua até que o refrigerante atinja o estado de líquido saturado . Construa o diagrama destes processos de resfriamento de determine o trabalho realizado do estado e do .

Olhando na fórmula já da pra matar uma reposta aqui:

Como do processo 1 ao 2 o volume é constante e a variação de uma constante é zero, logo:

Para determinar o trabalho realizado do estado , teremos que encontrar a pressão no estado final e a variação de volume, para isso:

Utilizar a condição do estado 1 e olhar nas tabela para encontrar seu volume.

Estado 1 com e :

Segundo enunciado sabendo disso e também que no estado 2 nós temos vapor saturado, ou seja , olharemos na tabela para encontrar a temperatura neste estado.

Para :

Como a pressão é constante no processo 2 ao 3, isso implica que a pressão no estado 2 é igual ao estado 3, logo:

E como só temos líquido saturado no estado 3, o volume é:

Com variáveis encontradas agora ficou tranquilo de aplicara fórmula do trabalho:

Substituindo valores:

Multiplicando pela massa:

Com o todos os cálculos feitos o diagrama , fica: