Enunciado

Termodinâmica - Van Wylen- Ed: 6º - Capítulo 4.Problemas - Ex. 59

Considere o processo composto pelas operações: a) expansão de a numa pressão constante e igual a e b) expansão desde o estado final da parte a até a com a pressão aumentando linearmente até . Construa o diagrama deste processo e termine o trabalho realizado pelo movimento de fronteira.

Passo 1

Fala galera, beleza?

Seguinte temos 3 estados, em que a letra (a) configura o e e a letra (b) o e 3, farei o diagrama para termos uma noção melhor do problema.

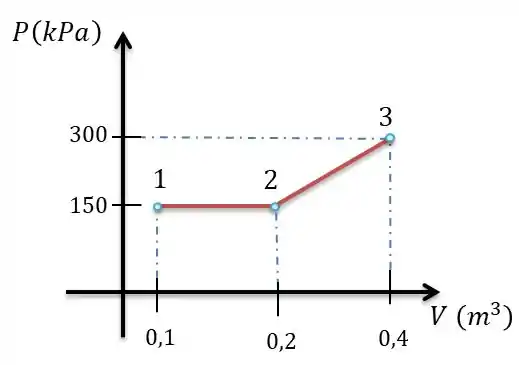
Galera o trabalho em relação à pressão e volume nada mais é que uma área integral, ou seja:

Sabendo disso fica claro que o nosso trabalho vai ser a integral sobe estas retas, ou melhor dizendo as áreas sobe as retas.

Passo 2

Calculando o trabalho:

De 1 a 2 temos a área de um quadrado e de 2 a 3 um trapézio.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um conjunto cilindro-pistão contém 3k g de ar. Inicialmente, a temperatura e a pressão no ar são iguais a 20 ° C e 300k P a . O ar é aquecido a pressão constante até que a sua temperatura atinja 600K

Um cilindro, que contém 1 k g de amônia, é provido de um êmbolo submetido a uma força externa variável. No estado inicial a amônia está a 2M P a e 180 ° C . O cilindro é resfriado e a força externa a

Considere um arranjo cilindro-pistão como mostra na F i g . P 4.64 Inicialmente, o arranjo contém 50k g de água a 200k P a e o volume interno do conjunto é igual a 0,1m 3 . O volume interno do conjunt

Um conjunto cilindro –pistão similar ao mostrado no Fig. P4.68 contém 0,1k g de água. Inicialmente, a pressão e título da água são respectivamente iguais a 100k P a e 25 % . A massa do pistão é tal qu