Um conjunto cilindro –pistão similar ao mostrado no Fig. P4.68 contém de água. Inicialmente, a pressão e título da água são respectivamente iguais a e . A massa do pistão é tal que torna-se necessária uma pressão de para equilibrá-lo. A água é então aquecida até que sua temperatura atinja . Determine a pressão final, o volume final e o trabalho realizado neste processo.
Passo 1
Fala pessoal, beleza? Bora resolver mais uma questão comigo?
Pessoal vamos ilustrar o nosso conjunto:
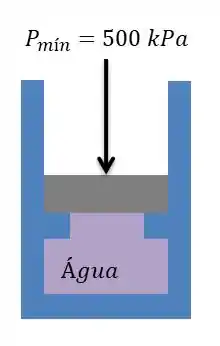
Temos água no estado inicial de e .
Então a água é aquecida até e a pressão mínima para elevar o pistão é de .
Temos que determinar volume, pressão no estado final e o trabalho realizado neste processo.
Passo 2
Galera para processos como este o volume é constante até o momento em que se atinge a pressão mínima, pressão mínima atingida temos que a pressão fica constante e o volume varia, ilustrando essa situação no diagrama fica mais ou menos assim:
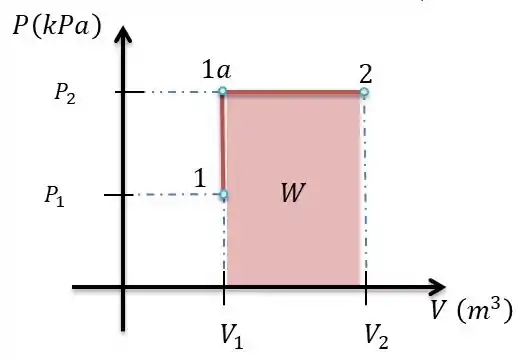
O trabalho é a área integrável do diagrama sobe a nossa função, colocando em fórmula:
Temos que determinar as avariáveis faltantes para encontrarmos o trabalho.
Passo 3
Para pressão final sabemos que e o enunciado nos fornece a temperatura final , tendo as condições de estado podemos determinar o volume específico.
Olhando na tabela com as condições ditas, temos:
Multiplicando pela massa de água:
Passo 4
Para determinar o volume inicial teremos que utilizar a fórmula do volume específico médio, que é a seguinte:
Utilizando a condição de estado , olhando na tabela , temos:
A diferença entre configura o volume da fase líquida vapor.
Substituindo os valores na fórmula do volume específico médio, temos:
Multiplicando pela massa:
Passo 5
Com doas as variáveis calculadas, vamos calcular o trabalho:
É isso galera, fecho.