Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 121

Desenvolva uma expressão para a eficiência térmica de um ciclo Brayton ideal com um regenerador ideal de 100 % de efetividade. Considere calores específicos constantes à temperatura ambiente.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

A eficiência térmica de um ciclo é dada por:

η = 1 - q s a i q e n t

Sabendo que em um regenerador temos que:

q s a i = c p T 6 - T 1

E:

q e n t = c p T 3 - T 5

Onde o diagrama T - s é dado abaixo:

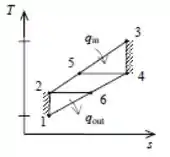
Vamos analisar os processos.

Passo 2

Para a expansão 3 → 4 , temos que:

T 4 T 3 = P 4 P 3 k - 1 k

Como:

P 4 P 3 = 1 r p

Substituindo os valores, temos que:

T 4 = T 3 1 r p k - 1 k

O processo 1 → 2 é uma compressão isentrópica, logo:

T 2 T 1 = P 2 P 1 k - 1 k

Temos que:

T 2 = T 1 ⋅ P 2 P 1 k - 1 k

Logo:

T 2 = T 1 ⋅ r p k - 1 k

Como a efetividade do regenerador é de 10 0 % , temos que:

T 5 = T 4

E:

T 6 = T 2

Agora, vamos desenvolver nossa expressão para a eficiência térmica.

Passo 3

A eficiência térmica é dada por:

η = 1 - c p T 6 - T 1 c p T 3 - T 5

η = 1 - T 6 - T 1 T 3 - T 5

Isolando T 1 e T 3 , temos que:

η = 1 - T 1 T 6 T 1 - 1 T 3 1 - T 5 T 3

Ou:

η = 1 - T 1 T 2 T 1 - 1 T 3 1 - T 4 T 3

Substituindo pelas expressões, temos que:

η = 1 - T 1 T 1 ⋅ r p k - 1 k T 1 - 1 T 3 1 - T 3 1 r p k - 1 k T 3

η = 1 - T 1 r p k - 1 k - 1 T 3 1 - 1 r p k - 1 k

Desenvolvendo, temos que:

η = T 1 T 3 r p - r p r p r p r p - 1 r p k - 1 k

Passo 4

Vamos considerar a seguinte expressão:

r p - r p r p r p r p - 1 r p

E r p = 3 , teremos que:

3 - 1 1 - 1 3

2 2 3 = 3

Ou seja:

r p - r p r p r p r p - 1 r p = r p

Portanto:

η = T 1 T 3 r p k - 1 k

Resposta

η = T 1 T 3 r p k - 1 k

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o P r o b .9 – 129 , considerando uma eficiência de 84 % , para cada estágio do compressor, e uma eficiência de 88 % , para cada estágio da turbina.
Reelabore o P r o b .9 – 131 E , considerando que cada compressor tenha uma eficiência isentrópica de 85 % e que cada turbina tem uma eficiência isentrópica de 90 % .
Uma turbina a gás tem dois estágios ideais de compressão, expansão, resfriamento intermediário e reaquecimento. O ar entra no primeiro compressor a 13p s i ae60° F ; a razão de pressão total (em todos
Considere um ciclo de turbina a gás ideal com dois estágios de compressão e dois estágios de expansão. A razão de pressão de cada estágio do compressor e da turbina é 3 . Ar entra em cadaestágio do co
Mostre que as eficiências isentrópicas de um compressor e de uma turbina podem ser escritas como as equações a seguir, considerando-se um gás ideal com calores específicos constantes: η c =( P 2 / P 1