Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 56
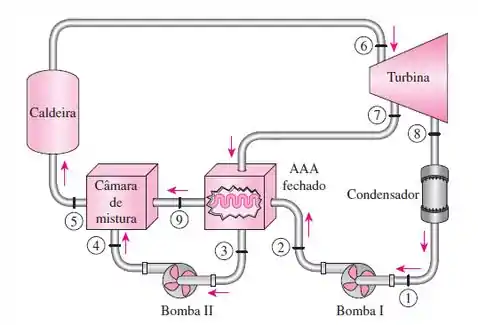
Determine a eficiência térmica do ciclo de Rankine regenerativo do Prob. 10-53, agora considerando que a eficiência isentrópica da turbina, antes e depois do ponto de extração de vapor, está a 90%, e que o condensador é sub-resfriado em 10 °C.
Passo 1
O esquema do enunciado não representa de maneira exata o que foi descrito no enunciado, pois foi dito que o regenerador descarrega água, estrangulada à pressão do condensador, para o condensador, então, redesenhando o ciclo, teremos:
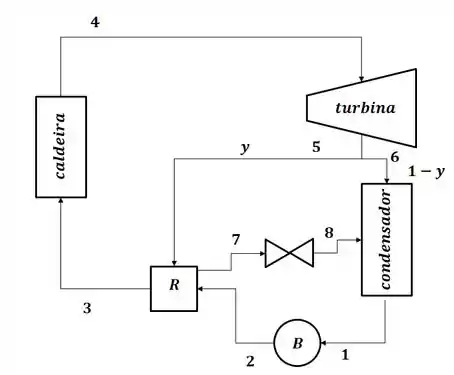
Beleza! A primeira coisa que temos que fazer é pegar o valor das propriedades nos pontos de interesse, então teremos:
No ponto 5, vamos considerar o processo primeiramente como isoentrópico, então temos:
Então, para esse ponto, o título será:
E, dessa forma, a entalpia será:
Agora, através das fórmulas de eficiência isentrópica podemos obter os valores reais para as entalpias nos pontos 5 e 6. Para os pontos 4 e 5, temos:
Substituindo os valores conhecidos:
Da mesma forma, para os pontos 4 e 6:
Substituindo os valores conhecidos:
Passo 2
Agora, continuando com os pontos de interesse, temos:
Como temos uma válvula de expansão entre 7 e 8, podemos considerar esse processo como isoentálpico, de forma que:
E, por fim, para o ponto 3, temos:
Agora vamos descobrir o valor do trabalho específico da bomba através de:
E, com isso a entalpia no ponto 2 pode ser calculada através do equilíbrio de energia na bomba, de forma que teremos:
Passo 3
Agora nós vamos aplicar o balanço de energia para o regenerador do passo 1, então, temos:
Nesse caso temos regime permanente, então , dessa forma a equação se torna:
E analisando o regenerador, teremos:
Com a relação mássica para o regenerador temos:
Substituindo os valores conhecidos, temos:
Com esse valor, agora podemos aplicar o equilíbrio de energia para a turbina e descobrir o trabalho produzido no sistema, então teremos:
Substituindo os valores conhecidos, temos:
Passo 4
Agora, vamos aplicar o balanço de energia específica para a caldeira, temos:
Substituindo os valores conhecidos, temos:
E, a eficiência do sistema será: