Duas correntes do mesmo gás ideal com fluxos de massa e temperaturas diferentes são misturadas em regime permanente em um dispositivo de mistura adiabático. Considerando calores específicos constantes, encontre a expressão mais simples para a temperatura da mistura escrita na forma:
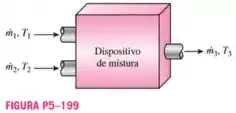
Passo 1

Este é um sistema em regime permanente, sem perdas, sem transferência de calor para o meio externo e sem trabalho. Então, a equação da energia pode ser resumida como:
Utilizando a entalpia, podemos expressar as energias dos fluxos de massa:
Como não há fluxo de calor ou trabalho que a entalpia pode ser expressa como: . Vamos aplicar isso:
Simplificando:
Isolando