A Fig. P9.39 exemplifica uma técnica utilizada na operação, em cargas parciais, de turbinas a vapor. Ela consiste em estrangular o vapor d’água de alimentação até uma pressão inferior à da linha. Admita que o vapor d’água na linha apresente pressão e temperaturas iguais a e e que a pressão na seção de descarga da turbina é .

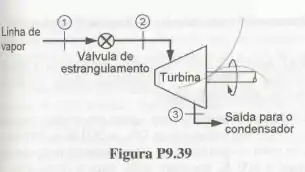
Considerando, ainda, que a expansão do fluido na turbina é adiabática e reversível, determine:

a) O trabalho, a plena carga, realizado pela turbina, por quilograma de vapor;

b) A pressão para a qual o vapor deve ser estrangulado para produzir do trabalho a plena carga;

c) Mostre os dois processos em diagramas .

Letra a)

Calculando o trabalho, a plena carga, realizado pela turbina.

Analisando a equação de energia e realizando as simplificações e desprezando as variações na energia cinética e potencial:

Pela Tabela B.1.3 obtemos os seguintes valores de entrada:

Pela Tabela B.1.2, obtemos as seguintes propriedades de saída:

Calculando o título de saída:

Calculando a entalpia de saída:

Agora sim, podemos calcular o trabalho:

Seguindo para a letra b!

Letra b)

Aqui, queremos a pressão para a qual o vapor deve ser estrangulado para produzir do trabalho a plena carga.

Calculando :

Calculando para obter :

Assim:

Analisando o processo, vemos que:

Buscando na Tabela B.1.3 e interpolando ente e , obtemos:

Vamos para o final do problema!

Letra c)

Colocando os dois processos em diagramas , temos:

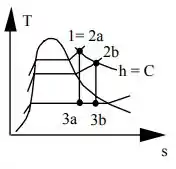
E assim, concluímos mais uma questão!

Até a próxima!