Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 90
Gás metano a 25 °C é queimado com a quantidade estequiométrica de ar a 25 °C durante um processo de combustão em regime permanente a 1 atm. Considerando que os gases do produto consistem em e , determine (a) a composição de equilíbrio dos gases de produto e (b) a temperatura de saída.
Passo 1
Tá legal! A primeira coisa que devemos fazer é escrever a equação de combustão de com a quantidade estequiométrica de ar será:
Nesse caso, e serão inertes. Comparando os termos dos dois lados da equação, para o balanço de temos:
E, para o balanço de , temos:
Substituindo a expressão encontrada para , temos:
Então, a equação de equilíbrio se torna:
E o número total de mols será:
Substituindo as expressões para e nessa equação, temos:
Passo 2
Beleza, agora vamos analisar a equação de dissociação do :
Então, temos:
Então, agora, com o auxílio da equação 16-15 apresentada nessa seção para a constante de equilíbrio:
Então, para o nosso caso, só não iremos considerar o que é inerte, então, a equação se torna:
Então, substituindo os valores conhecidos, temos:
E, substituindo os valores de e encontrados, temos:
Passo 3
Agora, para encontrar o valor de , vamos precisar realizar um processo iterativo pois ele depende da temperatura. Então, se aplicarmos o balanço de energia para a reação como foi feito no exemplo 16-6, com o auxílio da equação 15-6, lembrando que para o nosso caso, não temos calor entrando ou saindo do volume de controle, então temos o caso ideal onde a energia dos produtos é igual à dos reagentes. Dessa forma, teremos:
Então, uma vez que os reagentes estão no estado de referência padrão e para e , a equação acima se torna:
Agora devemos recorrer as tabelas do apêndice A para encontrar as entalpias de formação e a entalpia padrão a 298 K, dessa forma, teremos:
Então,substituindo esses valores na equação de equilíbrio, temos:
Só que agora, substituindo as expressões encontradas para e , temos:
Simplificando a expressão, chegamos em:
Passo 4
Agora, com as duas equações em função de , precisamos assumir duas temperaturas para encontrar os valores de , da temperatura de fato e encontrar a equação de equilíbrio. Então, assumindo:
Vamos recorrer à tabela A-28 para pegar o da dissociação de :
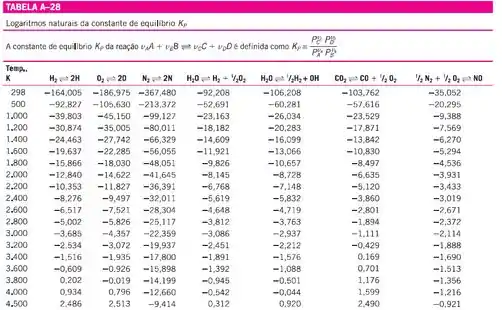
Substituindo esse valor na equação de encontrada no passo 2, temos:
Resolvendo a equação com a ajuda de uma calculadora, temos:
Agora, da equação de equilíbrio do passo 3, temos:
Substituindo o valor de e buscando os dados referentes as entalpias no apêndice A para , chegamos em:
Dessa forma o lado esquerdo da equação será:
Ainda não é igual ao valor 617328 do lado direito. Então, vamos calcular novamente , e as propriedades, só que agora, para .
Passo 5
Então, agora, teremos:
Substituindo esse valor na equação de encontrada no passo 2, temos:
Resolvendo a equação com a ajuda de uma calculadora, temos:
Agora, da equação de equilíbrio do passo 3, temos:
Substituindo o valor de e buscando os dados referentes as entalpias no apêndice A para , chegamos em:
Dessa forma o lado esquerdo da equação será:
Então, nesse caso, é um valor maior do que o desejado no lado direito da equação, então, agora, podemos interpolar com esses dados obtidos, pois sabemos que tanto a proporção , quanto a temperatura de interesse está entre os valores encontrados, então, teremos:
E o valor desejado será aquele em que o lado esquerdo da equação é igual a 617328, ou seja:
Então, interpolando com os valores acima, chegamos em:
Passo 6
Então, da equação de equilíbrio do passo 1, temos:
Substituindo o valor de , temos: