Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 6.Problemas - Ex. 78
Uma máquina térmica opera entre uma fonte a e um sumidouro a . Considerando que calor é fornecido a uma máquina térmica a uma taxa constante de , determine a potência máxima de saída dessa máquina.
Passo 1
Temos que a fonte e a temperatura de afundamento de um motor térmico e a taxa de fornecimento de calor são dadas. A potência máxima possível deste motor deve ser determinada.
Passo 2
Logo, a maior eficiência térmica que um motor térmico operando entre dois limites de temperatura especificados pode ter é a eficiência de Carnot, que é determinada a partir
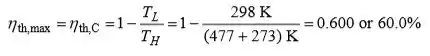
Então a potência máxima deste motor térmico é determinada a partir da definição de eficiência térmica a ser
Resposta
Exercícios de Livros Relacionados
Considere um ciclo de Carnot executado em um sistema fechado, em que o ar é utilizado como o fluido de trabalho. A pressão máxima no ciclo é de 800k P a , e a temperatura máxima é de 750K . Consideran
Considere um ciclo de Carnot executado em um sistema fechado com 0,6 kg de ar. Os limites de temperatura do ciclo são 300 K e 1.100 K, e as pressões mínima e máxima durante o ciclo são de 20 kPa e 3.0
Um ciclo de Carnot a gás ideal utiliza ar como fluido de trabalho, recebe calor de um reservatório térmico a 1.027° C , é repetido 1.500 vezes por minuto e tem uma razão de compressão igual a 12 . A r
Um gás ideal está contido em um arranjo pistão-cilindro e passa por um ciclo de potência descrito a seguir: 1-2 Compressão isentrópica de uma temperatura inicial T 1 = 20° C com uma razão de compressã
Por que o ciclo de Carnot não é um modelo realista para as usinas de potência a vapor?