Enunciado
Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 2.Problemas - Ex. 20
Projete um termômetro de mercúrio-em vidro para ser usado a temperaturas próximas a temperatura ambiente. O comprimento da coluna de mercúrio deverá variar um centímetro por grau C. Suponha que o coeficiente de dilatação volumétrica do mercúrio seja de , e que seja independente da temperatura para temperaturas próximas da temperatura ambiente, e que o coeficiente de dilatação volumétrica do vidro seja essencialmente nula.
Passo 1
Opa, beleza???
E aí, galera!?
De acordo com a figura 2.16, temos que...
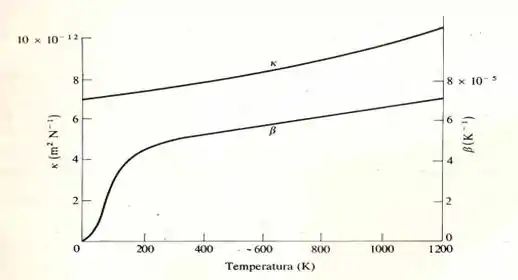
Passo 2
E sabemos também que a variação do volume de um sólido ou líquido é relativamente pequena, quando a pressão e a temperatura são variadas e, em primeira aproximação, podemos considerar como constante e igual a nas integrais da direita. Se e puderem ser tambem considerados constantes, então ficamos com a seguinte equação...
Essa é a equação que a gente vai ter que usar pra modelar nosso termômetro...
E no caso aqui, queremos que não mude, ou seja... O não pode mudar porque queremos que o nosso recipiente de vidro não altere seu volume...
Como estamos trabalhando em condições ambiente, vamos considerar...
E...
Logo;
E pronto! Temos nosso termômetro modelado aqui!