Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 100
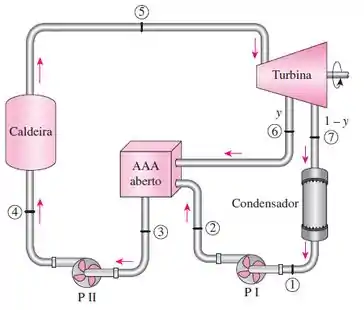
Considere uma usina de potência a vapor que opera em um ciclo de Rankine regenerativo e produz uma potência líquida de 150 MW. Vapor entra na turbina a 10 MPa e 500 °C, e no condensador, a 10 kPa. As eficiências isentrópicas da turbina e das bombas correspondem a 80% e 95% respectivamente. Vapor é extraído da turbina a 0,5 MPa para aquecer água de alimentação em um aquecedor aberto. A água deixa o aquecedor de água de alimentação como líquido saturado. Mostre o ciclo em um diagrama T-s e determine (a) o fluxo de massa de vapor na caldeira e (b) a eficiência térmica do ciclo. Determine também a destruição de exergia associada ao processo de regeneração. Considere uma temperatura da fonte de 1300 K e uma temperatura do sumidouro de 303 K.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo descrito no enunciado:
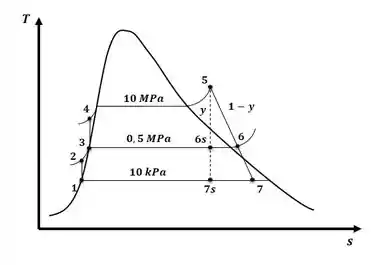
Agora, o que nós vamos fazer é encontrar o valor das propriedades de interesse com as temperaturas e pressões fornecidas no enunciado com a ajuda das tabelas do apêndice A, então, teremos:
Com isso, podemos encontrar o trabalho produzido pela bomba 1 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2:
Agora, continuando com as propriedades, temos:
Com isso, podemos encontrar o trabalho produzido pela bomba 2 através de:
E, com esse valor, aplicando o equilíbrio de energia para a bomba 2, podemos encontrar o valor da entalpia no ponto 4:
Agora, continuando com os pontos de interesse, temos:
Então, assumindo o processo 5-6 como isentrópico, temos que o título desse ponto nesse caso será:
E, com esse valor de título, podemos encontrar a entalpia para o caso isentrópico:
E, agora, através da definição de eficiência isentrópica da turbina, podemos encontrar a entalpia real do ponto 6:
Substituindo os valores conhecidos, temos:
E, com essa entalpia e a pressão no ponto 6 podemos encontrar a entropia nesse ponto, dada por:
Passo 2
Agora, repetindo a análise feita no ponto 6 para o ponto 7, temos:
Então, assumindo o processo 5-7 como isentrópico, temos que o título desse ponto nesse caso será:
E, com esse valor de título, podemos encontrar a entalpia para o caso isentrópico:
E, agora, através da definição de eficiência isentrópica da turbina, podemos encontrar a entalpia real do ponto 7:
Substituindo os valores conhecidos, temos:
Agora, com todas as propriedades determinadas, podemos aplicar o equilíbrio de energia para o aquecedor de água, então, teremos:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Escrevendo a equação anterior em função da fração mássica extraída para o aquecedor, temos:
Substituindo os valores conhecidos, temos:
Passo 3
Agora, podemos calcular o calor que entra no sistema pela caldeira, então, temos:
E o calor que sai do sistema através do condensador será:
Então, o trabalho líquido produzido por esse sistema será:
E, com o trabalho líquido específico e com a potência da usina fornecida no enunciado, podemos encontrar a vazão mássica de vapor no sistema:
Passo 4
E, a eficiência térmica pode ser encontrada através de:
Agora, sabemos que a destruição de exergia associada ao processo de regeneração pode ser dada por:
Em que a entropia gerada é dada por:
E, no nosso caso, teremos:
Substituindo essa expressão na equação para a exergia destruída, temos:
Substituindo os valores conhecidos, temos: