Na Fig. 10-114, é mostrado um ciclo a vapor de Rankine modificado ideal, utilizado para reaquecer dois aquecedores de água de alimentação fechados e uma unidade de processamento térmico. O ciclo de energia produz 300 MW de potência líquida. Os estados de saída do aquecedor de água de alimentação para a água de alimentação da caldeira e o vapor condensado são normalmente considerados estados ideais. A fração de massa que entra na turbina de alta pressão no estado 5 que é extraída para o funcionamento do aquecedor de água de alimentação a 1400 kPa é . Uma quantidade de 15% (z = 0,15) do vapor que entra na turbina de alta pressão é extraída da turbina de baixa pressão a 245 kPa para uso em uma unidade de processamento térmico a uma pressão constante; esse vapor é enviado para o aquecedor de água de alimentação fechado a 150 kPa por um purgador. Use os dados fornecidos nas tabelas seguintes para
(a) Esboçar o diagrama T-s para o ciclo ideal.
(b) Determinar a fração de massa que é extraída para o aquecedor de água de alimentação fechado operando a uma pressão de extração de 150 kPa para o ciclo ideal.
(c) Determinar o fluxo de massa através da caldeira, a taxa de calor fornecida para o processo e a eficiência de utilização da usina de cogeração.

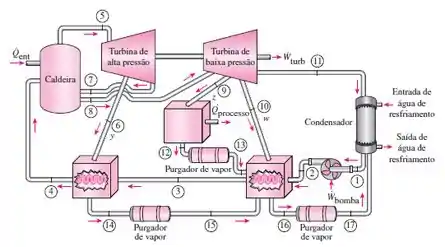
Passo 1
Vamos começar o exercício esboçando o diagrama T-s para o ciclo ideal conforme foi pedido na letra (a), então, teremos:
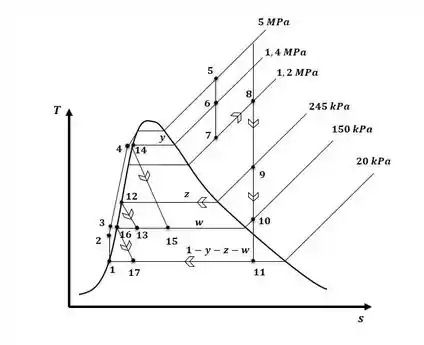
Passo 2
Beleza! Então agora o que temos que fazer é pegar o valor das propriedades nos pontos de interesse com o auxílio das tabelas termodinâmicas do apêndice A e das tabelas fornecidas no enunciado, então teremos:
Com esse valor, podemos encontrar o trabalho consumido pela bomba 1, então, temos:
Então, agora, aplicando o equilíbrio de energia para a bomba 1, podemos encontrar o valor da entalpia no ponto 2, assim, temos:
Continuando com as propriedades, temos:
Com isso, sabemos também que o purgador de vapor é um dispositivo isoentálpico, então, teremos:
Agora, continuando com as propriedades, temos:
Com isso, sabemos também que o purgador de vapor é um dispositivo isoentálpico, então, teremos:
E, como para o ponto 4 temos líquido comprimido, e ele se encontra à mesma temperatura do ponto 14, podemos aproximar sua entalpia como:
E, por fim, temos:
E, da mesma forma, temos o ponto 3 como líquido comprimido, à mesma temperatura do ponto 16, então, temos:
Agora, vamos aplicar um balanço de energia no aquecedor de água de alimentação fechado, então, temos:
Substituindo os valores conhecidos conseguimos encontrar o valor da fração mássica :
Passo 3
Para resolver a letra (c) precisamos encontrar o trabalho líquido produzido pelo sistema, então, através das turbinas, podemos encontrar o trabalho específico produzido em função das entalpias e das frações mássicas, então, teremos:
Substituindo os valores conhecidos:
Então, o trabalho líquido, que é dado pela diferença entre o trabalho produzido nas turbinas e aquele consumido pelas bombas, será:
Sendo assim, a vazão mássica do sistema pode ser encontrada a partir da potência produzida pela usina, então, temos:
Passo 4
Agora vamos calcular o calor que entra no sistema através da caldeira, lembrando que temos reaquecimento, então, teremos:
Substituindo os valores conhecidos, temos:
Agora, vamos calcular o calor que entra no sistema pela unidade de processamento térmico, então, teremos:
Substituindo os valores conhecidos, temos:
Então, o fator de utilização da usina será: